题目内容
5.平移坐标轴,使得抛物线y=x2-4x-3的顶点位于新坐标系x′O′y′的坐标原点,对称轴为y′轴,写出该抛物线在新坐标系中的方程.分析 由配方可得y=x2-4x-3=(x-2)2-7,顶点为(2,-7),对称轴为x=2,将x轴向下平移7个单位,y轴向右平移2个单位,可得新坐标系x′O'y′的方程.
解答 解:y=x2-4x-3=(x-2)2-7,
顶点为(2,-7),对称轴为x=2,
即有y+7=(x-2)2,
令x'=x-2,y'=y+7,
则有y'=x'2.
即将x轴向下平移7个单位,y轴向右平移2个单位,
可得该抛物线在新坐标系中的方程为x'2=y'.
点评 本题考查坐标轴的平移,考查抛物线的方程在两种坐标系下的形式,属于基础题.

练习册系列答案
相关题目
16.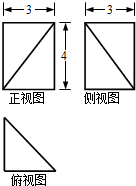 若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
 若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )| A. | 6cm3 | B. | 12cm3 | C. | 18cm3 | D. | 36cm3 |
 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,