题目内容
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点.
,E是PC的中点.

(Ⅰ)证明  平面EDB;
平面EDB;
(Ⅱ)求EB与底面ABCD所成的角的正切值.
【答案】
(Ⅰ)见解析;(Ⅱ)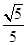 .
.
【解析】
试题分析:(Ⅰ)令AC、BD交于点O,连接OE,证明OE∥AP,即可证明AP∥面BDE;(Ⅱ)先找到直线与平面所成的角,令F是CD中点,又E是PC中点,连结EF,BF,可以证明EF⊥面ABCD,故∠EBF为面BE与面ABCD所成的角,在Rt⊿BEF中求出其正切值.
试题解析:(Ⅰ)令AC、BD交于点O,连接OE,∵O是AC中点,又E是PC中点
∴ OE∥AP 3分
又OE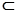 面BDE,AP
面BDE,AP 面BDE
5分
面BDE
5分
∴AP∥面BDE 6分
(Ⅱ)令F是CD中点,又E是PC中点,连结EF,BF
∴EF∥PD,又PD⊥面ABCD
∴EF⊥面ABCD 8分
∴∠EBF为面BE与面ABCD所成的角.
令PD=CD=2a
则CD=EF=a, BF=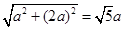 10分
10分
在Rt⊿BEF中,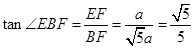
故BE与面ABCD所成角的正切是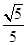 .
12分
.
12分
考点:线面平行的判定、直线与平面所成的角、勾股定理.

练习册系列答案
相关题目
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小. 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 是
是 的中点,
的中点, 是
是 的中点.
的中点.  ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.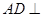 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面

 在棱
在棱 上.
上.
 时,求证
时,求证 平面
平面
 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.