题目内容
请阅读下列材料: 已知一系列函数有如下性质:
函数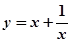 在
在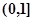 上是减函数,在
上是减函数,在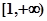 上是增函数;
上是增函数;
函数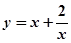 在
在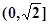 上是减函数,在
上是减函数,在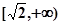 上是增函数;
上是增函数;
函数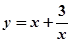 在
在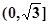 上是减函数,在
上是减函数,在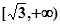 上是增函数;
上是增函数;
……
利用上述所提供的信息解决问题:
若函数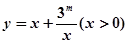 的值域是
的值域是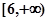 ,则实数
,则实数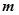 的值是 .
的值是 .
【答案】
2
【解析】
试题分析:根据题意,由于函数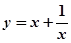 在
在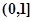 上是减函数,在
上是减函数,在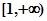 上是增函数;
上是增函数;
函数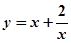 在
在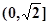 上是减函数,在
上是减函数,在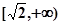 上是增函数;
上是增函数;
函数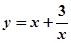 在
在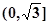 上是减函数,在
上是减函数,在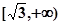 上是增函数;
上是增函数;
那么可知当函数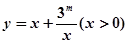 时 ,则有在
时 ,则有在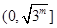 上是减函数,在
上是减函数,在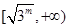 递增,那么可知其最小值在x=
递增,那么可知其最小值在x=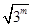 时取得,即函数值为6,解得2
时取得,即函数值为6,解得2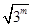 =6,实数
=6,实数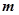 的值是2,故答案为2.
的值是2,故答案为2.
考点:函数的单调性
点评:主要是考查了函数的单调性的运用,体现了对钩函数的重要性,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥
(2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥ ,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答:
,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答: )2+
)2+ ,
, 时,u有最大值,umax=
时,u有最大值,umax= ,显然u没有最小值,
,显然u没有最小值, 时,g(x)有最小值4,没有最大值.
时,g(x)有最小值4,没有最大值. ,请提出此问题的一个结论,例如:求通项an.并给出正确解答.
,请提出此问题的一个结论,例如:求通项an.并给出正确解答. ;(2)请先阅读下列材料,然后根据要求回答问题.
;(2)请先阅读下列材料,然后根据要求回答问题. .
.