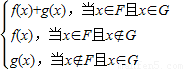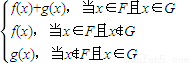Question

对定义域分别是F、G的函数y=f（x）、y=g（x），规定：函数h（x）=

f(x)+g(x)，当x∈F且x∈G   f(x)，当x∈F且x∉G   g(x)，当x∉F且x∈G

已知函数f（x）=x²，g（x）=alnx（a∈R）．
（1）求函数h（x）的解析式；
（2）对于实数a，函数h（x）是否存在最小值，如果存在，求出其最小值；如果不存在，请说明理由．

Answer 1

分析：（1）先求出两个函数各自的定义域，再代入分段函数的表达式即可求出函数h（x）的解析式；
（2）先求出第二段的最小值，再对第一段中的字母a分与0的三种关系分别讨论求出其最小值，再与第二段的最小值相比，最小的那个即为函数h（x）的最小值．

解答：解：（1）因为函数f（x）=x²的定义域F=（-∞，+∞），函数g（x）=alnx的定义域G=（0，+∞），
所以h（x）=

x2+alnx     x＞0 x2

x≤0（4分）
（2）当x≤0时，函数h（x）=x²单调递减，
所以函数h（x）在（-∞，0]上的最小值为h（0）=0．（5分）
当x＞0时，h（x）=x²+alnx．
若a=0，函数h（x）=x²在（0，+∞）上单调递增．此时，函数h（x）不存在最小值．（6分）
若a＞0，因为h′(x)=2x+

a

x

=

2x2+a

x

＞0，（7分）
所以函数h（x）=x²+alnx在（0，+∞）上单调递增．此时，函数h（x）不存在最小值．（8分）
若a＜0，因为h′(x)=

2x2+a

x

=

2(x+ - a 2 )(x- - a 2 )

x

，（9分）
所以函数h（x）=x²+alnx在(0，

- a 2

)上单调递减，在(

- a 2

，+∞)上单调递增．此时，函数h（x）的最小值为h(

- a 2

)．（10分）
因为h(

- a 2

)=-

a

2

+aln

- a 2

=-

a

2

+

a

2

ln(-

a

2

)=-

a

2

[1-ln(-

a

2

)]，（11分）
所以当-2e≤a＜0时，h(

- a 2

)≥0，当a＜-2e时，h(

- a 2

)＜0．（13分）
综上可知，当a＞0时，函数h（x）没有最小值；
当-2e≤a≤0时，函数h（x）的最小值为h（0）=0；
当a＜-2e时，函数h（x）的最小值为h(

- a 2

)=-

a

2

[1-ln(-

a

2

)]．（14分）

点评：本题主要考查函数解析式的求解及常用方法，利用导数求闭区间上函数的最值和分类讨论思想在解题中的应用，是对知识及思想方法的综合考查，属于中档题．