题目内容
已知 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且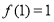 ,若
,若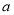 ,
,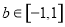 ,
, 时,有
时,有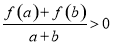 成立.
成立.
(1)判断 在[-1,1]上的单调性,并证明;
在[-1,1]上的单调性,并证明;
(2)解不等式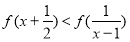 ;
;
(3)若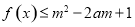 对所有的
对所有的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且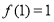 ,若
,若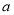 ,
,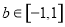 ,
, 时,有
时,有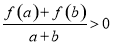 成立.
成立.
(1)判断 在[-1,1]上的单调性,并证明;
在[-1,1]上的单调性,并证明;
(2)解不等式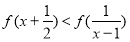 ;
;
(3)若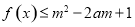 对所有的
对所有的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案