题目内容
已知直线l:5x+2y+3=0,经过点P(2,1)的直线l′到l的角等于45°,求直线l′的一般方程.
【答案】分析:设直线l′的斜率为k,直线l:5x+2y+3=0的斜率为k1,利用到角公式tan45°=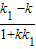 =1可求得k,从而可求直线l′的一般方程.
=1可求得k,从而可求直线l′的一般方程.
解答:解:∵直线l:5x+2y+3=0的斜率k1=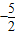 ,设直线l′的斜率为k,由题意得:tan45°=
,设直线l′的斜率为k,由题意得:tan45°=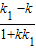 =1,
=1,
即(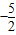 )-k=(1
)-k=(1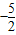 k),解得k=
k),解得k= ,
,
∵直线l′经过点P(2,1),由点斜式可得:
直线l′的方程为:7x-3y-11=0.
点评:本题考查两直线的到角问题,关键在于掌握到角公式,易错点在于到角公式与夹角公式混淆,属于中档题.
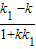 =1可求得k,从而可求直线l′的一般方程.
=1可求得k,从而可求直线l′的一般方程.解答:解:∵直线l:5x+2y+3=0的斜率k1=
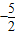 ,设直线l′的斜率为k,由题意得:tan45°=
,设直线l′的斜率为k,由题意得:tan45°=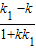 =1,
=1,即(
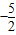 )-k=(1
)-k=(1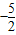 k),解得k=
k),解得k= ,
,∵直线l′经过点P(2,1),由点斜式可得:
直线l′的方程为:7x-3y-11=0.
点评:本题考查两直线的到角问题,关键在于掌握到角公式,易错点在于到角公式与夹角公式混淆,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目