题目内容
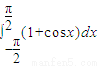 = ;若
= ;若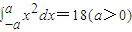 ,则a= .
,则a= .
【答案】分析:根据定积分的定义,找出三角函数的原函数然后代入计算即可求解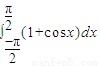 ;欲求∫-aax2dx=18(a>0)中的a值,先求积分得到关于a的等式,最后求解方程邓可.
;欲求∫-aax2dx=18(a>0)中的a值,先求积分得到关于a的等式,最后求解方程邓可.
解答:解: (x+sinx)
(x+sinx) 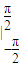 =
=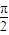 +1-(
+1-(  -1)=π+2,
-1)=π+2,
∵∫-aax2dx=18(a>0)
∴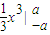 =18,
=18,
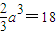 ⇒a=3,
⇒a=3,
故答案为π+2;3.
点评:此题考查定积分的性质及其计算,是高中新增的内容,要掌握定积分基本的定义和性质,解题的关键是找出原函数.
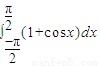 ;欲求∫-aax2dx=18(a>0)中的a值,先求积分得到关于a的等式,最后求解方程邓可.
;欲求∫-aax2dx=18(a>0)中的a值,先求积分得到关于a的等式,最后求解方程邓可.解答:解:
 (x+sinx)
(x+sinx) 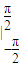 =
=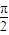 +1-(
+1-(  -1)=π+2,
-1)=π+2,∵∫-aax2dx=18(a>0)
∴
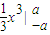 =18,
=18,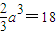 ⇒a=3,
⇒a=3,故答案为π+2;3.
点评:此题考查定积分的性质及其计算,是高中新增的内容,要掌握定积分基本的定义和性质,解题的关键是找出原函数.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目