题目内容
(本小题满分12分)
某大学高等数学老师上学期分别采用了 两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如下:
两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如下:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学,求成绩为90分的同学被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| | 甲班 | 乙班 | 合计 |
| 优秀 | | | |
| 不优秀 | | | |
| 合计 | | | |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中
其中 )
) (Ⅳ)从乙班高等数学成绩不低于85分的同学中抽取2人,成绩不低于90分的同学得奖金100元,否则得奖金50元,记
 为这2人所得的总奖金,求
为这2人所得的总奖金,求 的分布列和数学期望。
的分布列和数学期望。
(1) 乙班的平均分高 (2) 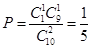
(3) 在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关
(4)150
解析试题分析:解:
(Ⅰ)甲班高等数学成绩集中于60-90分之间,而乙班数学成绩集中于80-100分之间,所以乙班的平均分高 ………………………………2分
(Ⅱ)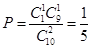 ………………………………4分
………………………………4分
(Ⅲ)
………………………………6分 甲班 乙班 合计 优秀 3 10 13 不优秀 17 10 27 合计 20 20 40 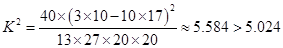 ,因此在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关。………………………………8分
,因此在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关。………………………………8分
(Ⅳ)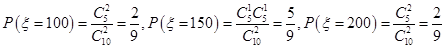
所以
………………………………10分
100元 150元 200元 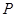
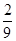
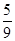
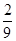
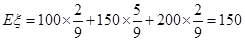 (元) ………………………………12分
(元) ………………………………12分
考点:茎叶图,独立性检验、分布列等知识的运用
点评:解题的关键是理解茎叶图表示数字特征的求解,以及分布列的求和和数学期望值的运用。属于基础题。

某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽y(颗) | 23 | 25 | 30 | 26 | 16 |
回归直线方程参考公式:

 ,
, 

(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
 ;
;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则
认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(3)请预测温差为14℃的发芽数。
某市居民1999~2003年货币收入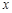 与购买商品支出
与购买商品支出 的统计资料如下表所示:单位:亿元
的统计资料如下表所示:单位:亿元
| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
货币收入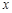 | 40 | 42 | 44 | 47 | 50 |
购买商品支出 | 33 | 34 | 36 | 39 | 41 |

(Ⅱ)已知
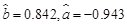 ,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元? (本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25 | [25,35 | [35,45 | [45,55 | [55,65 | [65,75 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 |  |  | |
| 不赞成 |  |  | |
| 合计 | | | |
(2)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
 ,求随机变量
,求随机变量 的分布列。
的分布列。附:


(本题满分12分)
对某校高二年级学生参加社会实践活动次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践活动的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
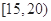 | 26 | n |
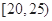 | m | P |
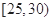 | 1 | 0.025 |
| 合计 | M | 1 |
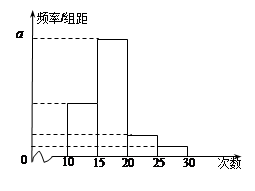
(Ⅰ)求出表中M,P及图中
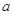 的值;
的值;(Ⅱ)在所取样本中,从参加社会实践活动的次数不少于20次的学生中任选2人,求恰有一人参加社会实践活动次数在区间
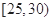 内的概率.
内的概率. 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
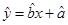 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。(相关公式:
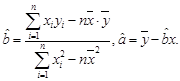 )
)  .
.
 分内的人数.
分内的人数.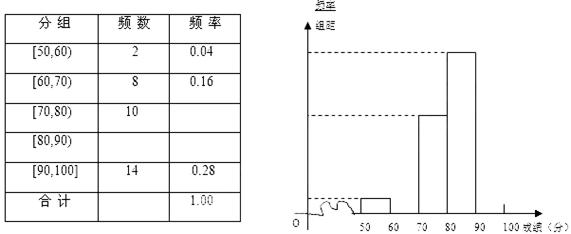
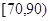 段的有多少人;
段的有多少人;