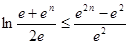题目内容
(14分)设函数 ,其中
,其中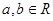
(1)当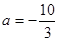 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(2)若函数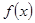 仅在
仅在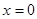 处有极值,求
处有极值,求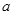 的取值范围;
的取值范围;
(3)若对于任意的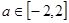 ,不等式
,不等式 在[-1,1]上恒成立,求b的取值范围.
在[-1,1]上恒成立,求b的取值范围.
(1)f(x)在(0, 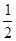 ),(2,+∞)内是增函数,在(-∞,0),(
),(2,+∞)内是增函数,在(-∞,0),( 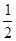 ,2)内是减函数.
,2)内是减函数.
(2)
(3)(-∞,-4]
【解析】解 (1)f′(x)=4x3+3ax2+4x=x(4x2+3ax+4). 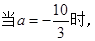 f′(x)=x(4x2-10x+4)=2x(2x-1)(x-2).?
f′(x)=x(4x2-10x+4)=2x(2x-1)(x-2).?
令f′(x)=0,解得
x1=0, x2=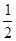 ,x3=2当x变化时,f′(x),f(x)的变化情况如下表:
,x3=2当x变化时,f′(x),f(x)的变化情况如下表:
|
x |
(-∞,0) |
0 |
|
|
|
2 |
(2,+∞) |
|
f′(x) |
- |
0 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以f(x)在(0, 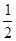 ),(2,+∞)内是增函数,在(-∞,0),(
),(2,+∞)内是增函数,在(-∞,0),( 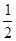 ,2)内是减函数.?
,2)内是减函数.?
(2)f′(x)=x(4x2+3ax+4),显然x=0不是方程4x2+3ax+4=0的根.
为使f(x)仅在x=0处有极值,必须有4x2+3ax+4≥0恒成立,即有Δ=9a2-64≤0. 解此不等式,得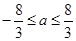 这时,f(0)=b是唯一极值. 因此满足条件的a的取值范围是
这时,f(0)=b是唯一极值. 因此满足条件的a的取值范围是 .
.
3)由条件a∈[-2,2]可知Δ=9a2-64<0,从而4x2+3ax+4>0恒成立.
当x<0时,f′(x)<0;当x>0时,f′(x)>0.因此函数f(x)在[-1,1]上的最大值是f(1)与f(-1)两者中的较大者.
为使对任意的a∈[-2,2],不等式f(x)≤1在[-1,1]上恒成立,当且仅当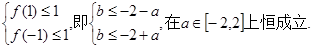 所以b≤-4,
所以b≤-4,
因此满足条件的b的取值范围是(-∞,-4].

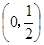
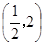
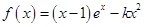 (其中
(其中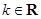 ).
).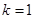 时,求函数
时,求函数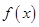 的单调区间和极值;
的单调区间和极值;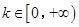 时,函数
时,函数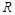 上有且只有一个零点.
上有且只有一个零点.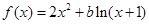 ,其中
,其中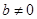 .
.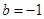 时,求在曲线
时,求在曲线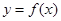 上一点
上一点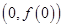 处的切线方程;
处的切线方程;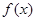 的极值点。
的极值点。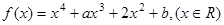 ,其中
,其中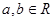
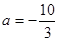 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;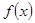 仅在
仅在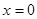 处有极值,求
处有极值,求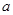 的取值范围;
的取值范围; ,不等式
,不等式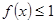 在[-1,1]上恒成立,求b的取值范围.
在[-1,1]上恒成立,求b的取值范围.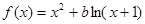 ,其中
,其中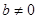
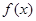 的单调增区间
的单调增区间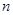 ,证明:
,证明: