题目内容
9.函数f(x+)=sinx-f(x),当0≤x<时,f(x)=1,则f()=( )| A. | 1 | B. | - | C. | -1 | D. |
分析 直接利用已知条件,化简所求表达式,求解即可.
解答 解:函数f(x+)=sinx-f(x),当0≤x<时,f(x)=1,
则f()=f()
=sin-f()
=sin-f(+)
=sin-sin+f()
=sin-sin+f(+)
=sin-sin+sin-f()
=-1
=-.
故选:B.
点评 本题考查三角函数的化简求值抽象函数的应用,考查计算能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0, 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.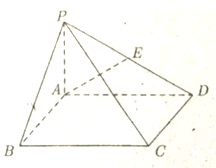 在四棱锥P-ABCD中,PA⊥底面ABCD,PA=1,底面ABCD是正方形,E是PD的中点,PD与底面ABCD所成的角为
在四棱锥P-ABCD中,PA⊥底面ABCD,PA=1,底面ABCD是正方形,E是PD的中点,PD与底面ABCD所成的角为