题目内容
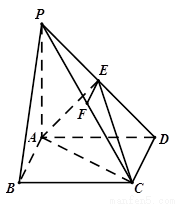
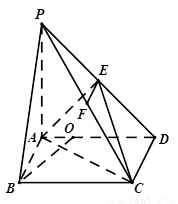
如图,在四棱锥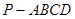 中,
中,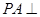 底面
底面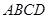 ,四边形
,四边形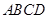 为长方形,
为长方形,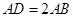 ,点
,点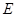 、
、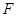 分别是线段
分别是线段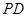 、
、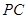 的中点.
的中点.
(Ⅰ)证明: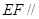 平面
平面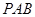 ;
;
(Ⅱ)在线段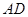 上是否存在一点
上是否存在一点 ,使得
,使得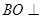 平面
平面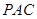 ,若存在,请指出点
,若存在,请指出点 的位置,并证明
的位置,并证明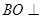 平面
平面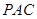 ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】
(Ⅰ)见解析;(Ⅱ) 在线段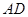 上存在一点
上存在一点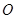 ,使得
,使得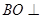 平面
平面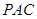 ,此时点
,此时点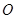 为线段
为线段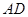 的四等分点。理由见解析。
的四等分点。理由见解析。
【解析】(1)由三角形中位线的性质得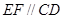 ,又
,又 ,所以
,所以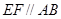 .根据线面平行的判定定理可证得结论;(2)由已知得
.根据线面平行的判定定理可证得结论;(2)由已知得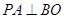 ,关键是证
,关键是证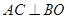 ,当点
,当点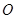 为线段
为线段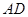 的四等分点时,有△
的四等分点时,有△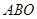 ∽△
∽△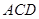 ,可得
,可得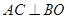 .
.
(Ⅰ)∵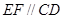 ,
, ,∴
,∴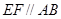 ,
,
又∵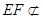 平面
平面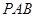 ,
,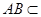 平面
平面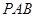 ,
,
∴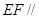 平面
平面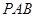 .
……………………6分
.
……………………6分
(Ⅱ) 在线段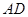 上存在一点
上存在一点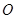 ,使得
,使得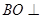 平面
平面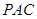 ,
,
此时点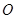 为线段
为线段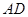 的四等分点,
的四等分点,
且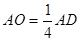 , …………………… 8分
, …………………… 8分
∵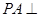 底面
底面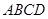 ,∴
,∴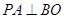 ,
,
又∵长方形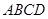 中,△
中,△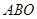 ∽△
∽△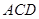 ,∴
,∴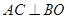 ,······································ 10分
,······································ 10分
又∵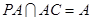 ,∴
,∴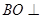 平面
平面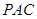 . 12分
. 12分

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小. 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 是
是 的中点,
的中点, 是
是 的中点.
的中点.  ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.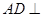 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面

 在棱
在棱 上.
上.
 时,求证
时,求证 平面
平面
 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.