题目内容
己知
，则m等于（ ）A．
B．
C．
D．
【答案】分析：设
，求出f（t）=4t+7，进而得到f（m）=4m+7，由此能够求出m．
解答：解：设
，则x=2t+2，
∴f（t）=4t+7，∴f（m）=4m+7=6，
解得m=-
．
故选A．
点评：本题考查函数值的求法，解题时要认真审题，仔细求解，注意公式的灵活运用．
，求出f（t）=4t+7，进而得到f（m）=4m+7，由此能够求出m．解答：解：设
，则x=2t+2，∴f（t）=4t+7，∴f（m）=4m+7=6，
解得m=-
．故选A．
点评：本题考查函数值的求法，解题时要认真审题，仔细求解，注意公式的灵活运用．
练习册系列答案
相关题目
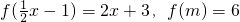，则m等于
，则m等于（ ）
，则m等于（ ）
，则m等于（ ）
