题目内容
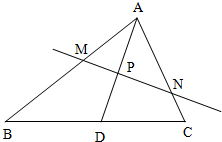 在△ABC中,已知P为中线AD的中点.过点P作一直线分别和边AB、AC交于点M、N,设
在△ABC中,已知P为中线AD的中点.过点P作一直线分别和边AB、AC交于点M、N,设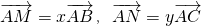 ,
,
(Ⅰ)求证:△ABC的面积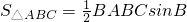 ;
;
(Ⅱ)求当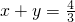 时,求△AMN与△ABC的面积比.
时,求△AMN与△ABC的面积比.
证明:(Ⅰ):当∠B是直角时,S△ABC=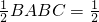 BA•BC•sinB,结论成立,
BA•BC•sinB,结论成立,
当∠B不是直角时,过A作直线BC的垂线,垂足为H,
若∠B是锐角,则AH=AB•sinB,∴S△ABC=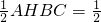 BA•BC•sinB,
BA•BC•sinB,
若∠B是钝角,则AH=AB•sin(π-B)=AB•sinB∴S△ABC=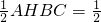 BA•BC•sinB.
BA•BC•sinB.
综上所述,S△ABC= BA•BC•sinB的结论成立.------------------(6分)
BA•BC•sinB的结论成立.------------------(6分)
(Ⅱ)因为D为BC的中点,P为AD的中点,∴ ,∴
,∴ )--------(8分)
)--------(8分)
∴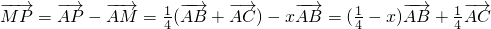
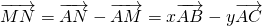 ,
,
有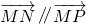 知,存在实数λ,使得
知,存在实数λ,使得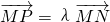 ,
,
可得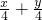 =xy,又x+y=
=xy,又x+y= ,xy=
,xy= ,-----------------(13分)
,-----------------(13分)
由(Ⅰ)知 .-----------------(16分)
.-----------------(16分)
分析:(Ⅰ)通过对当∠B是直角时,当∠B不是直角时,过A作直线BC的垂线,垂足为H,若∠B是锐角,若∠B是钝角,分别证明△ABC的面积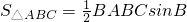 ;
;
(Ⅱ)由D为BC的中点,P为AD的中点,通过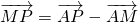 ,
,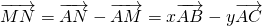 ,利用
,利用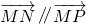 知,存在实数λ,使得
知,存在实数λ,使得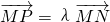 ,得到x+y=
,得到x+y= ,xy=
,xy= ,由(Ⅰ)求出
,由(Ⅰ)求出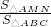 的值.
的值.
点评:本题考查向量的基本运算,分类讨论的思想,三角形的面积的求法,向量之间的转化是解题的关键,考查计算能力.
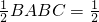 BA•BC•sinB,结论成立,
BA•BC•sinB,结论成立,当∠B不是直角时,过A作直线BC的垂线,垂足为H,
若∠B是锐角,则AH=AB•sinB,∴S△ABC=
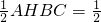 BA•BC•sinB,
BA•BC•sinB,若∠B是钝角,则AH=AB•sin(π-B)=AB•sinB∴S△ABC=
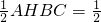 BA•BC•sinB.
BA•BC•sinB.综上所述,S△ABC=
 BA•BC•sinB的结论成立.------------------(6分)
BA•BC•sinB的结论成立.------------------(6分)(Ⅱ)因为D为BC的中点,P为AD的中点,∴
 ,∴
,∴ )--------(8分)
)--------(8分)∴
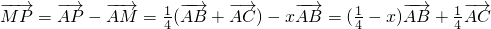
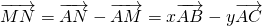 ,
,有
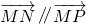 知,存在实数λ,使得
知,存在实数λ,使得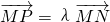 ,
,可得
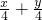 =xy,又x+y=
=xy,又x+y= ,xy=
,xy= ,-----------------(13分)
,-----------------(13分)由(Ⅰ)知
 .-----------------(16分)
.-----------------(16分)分析:(Ⅰ)通过对当∠B是直角时,当∠B不是直角时,过A作直线BC的垂线,垂足为H,若∠B是锐角,若∠B是钝角,分别证明△ABC的面积
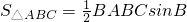 ;
;(Ⅱ)由D为BC的中点,P为AD的中点,通过
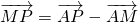 ,
,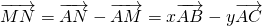 ,利用
,利用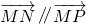 知,存在实数λ,使得
知,存在实数λ,使得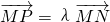 ,得到x+y=
,得到x+y= ,xy=
,xy= ,由(Ⅰ)求出
,由(Ⅰ)求出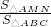 的值.
的值.点评:本题考查向量的基本运算,分类讨论的思想,三角形的面积的求法,向量之间的转化是解题的关键,考查计算能力.

练习册系列答案
相关题目
 在△ABC中,已知P为中线AD的中点.过点P作一直线分别和边AB、AC交于点M、N,设
在△ABC中,已知P为中线AD的中点.过点P作一直线分别和边AB、AC交于点M、N,设