题目内容
一动圆与已知⊙O1: 相外切,与⊙O2:
相外切,与⊙O2: 相内切.
相内切.(Ⅰ)求动圆圆心的轨迹C;
(Ⅱ)若轨迹C与直线y=kx+m (k≠0)相交于不同的两点M、N,当点A(0,-1)满足|
 |=|
|=| |时,求m的取值范围.
|时,求m的取值范围.
【答案】分析:(Ⅰ)由动圆与已知⊙O1: 相外切,可得到|MO1|=1+R,由与⊙O2:
相外切,可得到|MO1|=1+R,由与⊙O2: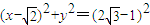 相内切,可得,|MO2|=(2
相内切,可得,|MO2|=(2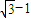 )-R,从而|MO1|+|MO2|=2
)-R,从而|MO1|+|MO2|=2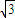 .根据椭圆的定义可得M点的轨迹是以O1,O2为焦点的椭圆,故可求椭圆的标准方程.
.根据椭圆的定义可得M点的轨迹是以O1,O2为焦点的椭圆,故可求椭圆的标准方程.
(Ⅱ)直线y=kx+m与椭圆的标准方程联立,消去y得(3k2+1)x2+6mkx+3(m2-1)=0,所以△=-12m2+36k2+12>0⇒m2<3k2+1.设P为MN的中点,则MN⊥AP,可得2m=3k2+1,从而可求m的取值范围.
解答:解:(Ⅰ)设动圆圆心为M(x,y),半径为R,则由题设条件,可知:
|MO1|=1+R,|MO2|=(2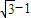 )-R,∴|MO1|+|MO2|=2
)-R,∴|MO1|+|MO2|=2 .
.
由椭圆定义知:M在以O1,O2为焦点的椭圆上,且 ,
,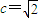 ,b2=a2-c2=3-2=1,故动圆圆心的轨迹方程为
,b2=a2-c2=3-2=1,故动圆圆心的轨迹方程为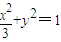 .…(4分)
.…(4分)
(Ⅱ)设P为MN的中点,联立方程组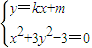 ,⇒(3k2+1)x2+6mkx+3(m2-1)=0.△=-12m2+36k2+12>0⇒m2<3k2+1 …(1)…(6分)
,⇒(3k2+1)x2+6mkx+3(m2-1)=0.△=-12m2+36k2+12>0⇒m2<3k2+1 …(1)…(6分)
又
由MN⊥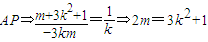 …(2)…(9分)
…(2)…(9分) .故
.故 .…(12分)
.…(12分)
点评:本题考查圆与圆的位置关系,椭圆的定义和标准方程,得到|MO1|+|MO2|>|O1O2|是解题的关键.考查直线与椭圆的位置关系,掌握其常规方法.
 相外切,可得到|MO1|=1+R,由与⊙O2:
相外切,可得到|MO1|=1+R,由与⊙O2: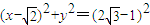 相内切,可得,|MO2|=(2
相内切,可得,|MO2|=(2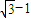 )-R,从而|MO1|+|MO2|=2
)-R,从而|MO1|+|MO2|=2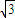 .根据椭圆的定义可得M点的轨迹是以O1,O2为焦点的椭圆,故可求椭圆的标准方程.
.根据椭圆的定义可得M点的轨迹是以O1,O2为焦点的椭圆,故可求椭圆的标准方程.(Ⅱ)直线y=kx+m与椭圆的标准方程联立,消去y得(3k2+1)x2+6mkx+3(m2-1)=0,所以△=-12m2+36k2+12>0⇒m2<3k2+1.设P为MN的中点,则MN⊥AP,可得2m=3k2+1,从而可求m的取值范围.
解答:解:(Ⅰ)设动圆圆心为M(x,y),半径为R,则由题设条件,可知:
|MO1|=1+R,|MO2|=(2
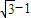 )-R,∴|MO1|+|MO2|=2
)-R,∴|MO1|+|MO2|=2 .
.由椭圆定义知:M在以O1,O2为焦点的椭圆上,且
 ,
,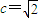 ,b2=a2-c2=3-2=1,故动圆圆心的轨迹方程为
,b2=a2-c2=3-2=1,故动圆圆心的轨迹方程为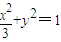 .…(4分)
.…(4分)(Ⅱ)设P为MN的中点,联立方程组
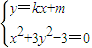 ,⇒(3k2+1)x2+6mkx+3(m2-1)=0.△=-12m2+36k2+12>0⇒m2<3k2+1 …(1)…(6分)
,⇒(3k2+1)x2+6mkx+3(m2-1)=0.△=-12m2+36k2+12>0⇒m2<3k2+1 …(1)…(6分)又

由MN⊥
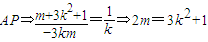 …(2)…(9分)
…(2)…(9分) .故
.故 .…(12分)
.…(12分)点评:本题考查圆与圆的位置关系,椭圆的定义和标准方程,得到|MO1|+|MO2|>|O1O2|是解题的关键.考查直线与椭圆的位置关系,掌握其常规方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 相外切,与⊙O2:
相外切,与⊙O2: 相内切.
相内切. |=|
|=| |时,求m的取值范围.
|时,求m的取值范围.