题目内容
如图,函数 的图象与y轴交于点
的图象与y轴交于点 ,且在该点处切线的斜率为-2.
,且在该点处切线的斜率为-2.(1)求θ和ω的值;
(2)已知点
 ,点P是该函数图象上一点,点Q(x,y)是PA的中点,当
,点P是该函数图象上一点,点Q(x,y)是PA的中点,当 ,
, 时,求x的值.
时,求x的值.
【答案】分析:(1)根据(0,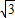 )以及θ的范围,求θ,利用导数和斜率的关系求ω的值;
)以及θ的范围,求θ,利用导数和斜率的关系求ω的值;
(2)利用点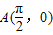 ,点Q(x,y)求出P,点P是该函数图象上一点,代入表达式,利用
,点Q(x,y)求出P,点P是该函数图象上一点,代入表达式,利用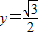 ,
,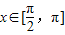 ,求x的值.
,求x的值.
解答:解:(1)将x=0,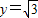 代入函数y=2cos(ωx+θ)得
代入函数y=2cos(ωx+θ)得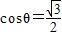 ,
,
因为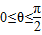 ,所以
,所以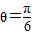 .
.
又因为y'=-2ωsin(ωx+θ),y'|x=0=-2,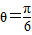 ,所以ω=2,
,所以ω=2,
因此 .
.
(2)因为点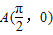 ,Q(x,y)是PA的中点,
,Q(x,y)是PA的中点,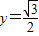 ,
,
所以点P的坐标为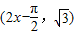 .
.
又因为点P在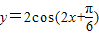 的图象上,所以
的图象上,所以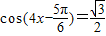 .
.
因为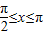 ,所以
,所以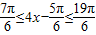 ,
,
从而得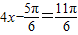 或
或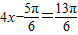 .
.
即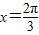 或
或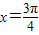 .
.
点评:本题考查y=Asin(ωx+φ)中参数的物理意义,导数的运算,考查分析问题解决问题的能力,是中档题.
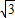 )以及θ的范围,求θ,利用导数和斜率的关系求ω的值;
)以及θ的范围,求θ,利用导数和斜率的关系求ω的值;(2)利用点
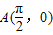 ,点Q(x,y)求出P,点P是该函数图象上一点,代入表达式,利用
,点Q(x,y)求出P,点P是该函数图象上一点,代入表达式,利用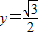 ,
,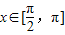 ,求x的值.
,求x的值.解答:解:(1)将x=0,
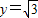 代入函数y=2cos(ωx+θ)得
代入函数y=2cos(ωx+θ)得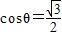 ,
,因为
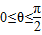 ,所以
,所以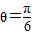 .
.又因为y'=-2ωsin(ωx+θ),y'|x=0=-2,
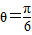 ,所以ω=2,
,所以ω=2,因此
 .
.(2)因为点
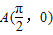 ,Q(x,y)是PA的中点,
,Q(x,y)是PA的中点,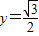 ,
,所以点P的坐标为
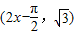 .
.又因为点P在
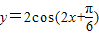 的图象上,所以
的图象上,所以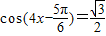 .
.因为
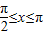 ,所以
,所以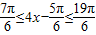 ,
,从而得
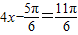 或
或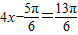 .
.即
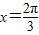 或
或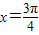 .
.点评:本题考查y=Asin(ωx+φ)中参数的物理意义,导数的运算,考查分析问题解决问题的能力,是中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

 的图象与y轴交于点
的图象与y轴交于点 ,且在该点处切线的斜率为-2.
,且在该点处切线的斜率为-2. ,点P是该函数图象上一点,点Q(x,y)是PA的中点,当
,点P是该函数图象上一点,点Q(x,y)是PA的中点,当 ,
, 时,求x的值.
时,求x的值.
 的图象与y轴交于点
的图象与y轴交于点 ,且在该点处切线的斜率为-2.
,且在该点处切线的斜率为-2. ,点P是该函数图象上一点,点Q(x,y)是PA的中点,当
,点P是该函数图象上一点,点Q(x,y)是PA的中点,当 ,
, 时,求x的值.
时,求x的值.
 的图象与y轴交于点
的图象与y轴交于点 ,且在该点处切线的斜率为-2.
,且在该点处切线的斜率为-2. ,点P是该函数图象上一点,点Q(x,y)是PA的中点,当
,点P是该函数图象上一点,点Q(x,y)是PA的中点,当 ,
, 时,求x的值.
时,求x的值.