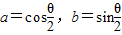题目内容
给出下列的四个式子:①
,②
,③
,④
;已知其中至少有两个式子的值与tanθ的值相等,则( )
| 1-a |
| b |
| 1+a |
| b |
| b |
| 1+a |
| b |
| 1-a |
分析:利用正切函数的2倍角公式对A、B、C、D四个选项进行一一判断,从而进行求解;
解答:解:已知①
,②
,③
,④
;
A、∵tanθ=
=
=
,
∴a=cos2θ,b=sin2θ时,
式子①③与tanθ的值相等,
故A正确.
B、a=sin2θ,b=cos2θ,因为tanθ=
=
=
,可得
tanθ=
=
,故B错误;
C、∵a=sin
,b=cos
tan
=
,tanθ=
=
=
,故C错误;
D、a=cos
,b=sin
,可得tan
=
,tanθ=
=
,
故D错误;
故选A;
| 1-a |
| b |
| 1+a |
| b |
| b |
| 1+a |
| b |
| 1-a |
A、∵tanθ=
| sinθ |
| cosθ |
| sin2θ |
| 1+cos2θ |
| 1-cos2θ |
| sin2θ |
∴a=cos2θ,b=sin2θ时,
式子①③与tanθ的值相等,
故A正确.
B、a=sin2θ,b=cos2θ,因为tanθ=
| sinθ |
| cosθ |
| sin2θ |
| 1+cos2θ |
| 1-cos2θ |
| sin2θ |
tanθ=
| a |
| 1+b |
| 1-b |
| a |
C、∵a=sin
| θ |
| 2 |
| θ |
| 2 |
tan
| θ |
| 2 |
| a |
| b |
2tan
| ||
| 1-tan2θ |
2×
| ||
1-(
|
| 2ab |
| b2-a2 |
D、a=cos
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| b |
| a |
2tan
| ||
| 1-tan2θ |
| 2ab |
| a2-b2 |
故D错误;
故选A;
点评:此题主要考查正切函数的二倍角公式及其应用,是一道基础题,解题过程比较复杂,需要一一验证;

练习册系列答案
相关题目
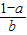 ,②
,②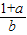 ,③
,③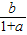 ,④
,④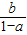 ;已知其中至少有两个式子的值与tanθ的值相等,则( )
;已知其中至少有两个式子的值与tanθ的值相等,则( )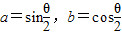
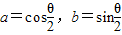
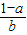 ,②
,②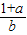 ,③
,③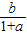 ,④
,④ ;已知其中至少有两个式子的值与tanθ的值相等,则( )
;已知其中至少有两个式子的值与tanθ的值相等,则( )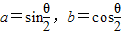
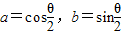
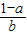 ,②
,②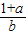 ,③
,③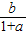 ,④
,④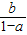 ;已知其中至少有两个式子的值与tanθ的值相等,则( )
;已知其中至少有两个式子的值与tanθ的值相等,则( )

 ,②
,②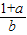 ,③
,③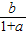 ,④
,④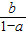 ;已知其中至少有两个式子的值与tanθ的值相等,则( )
;已知其中至少有两个式子的值与tanθ的值相等,则( )