题目内容
设数列 的前n项积为
的前n项积为 ;数列
;数列 的前n项和为
的前n项和为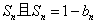 .
.
(1)设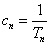 .①证明数列
.①证明数列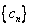 成等差数列;②求证数列
成等差数列;②求证数列 的通项公式;
的通项公式;
(2)若 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】
【解析】(1)①由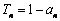 得:
得: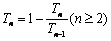 ,
,
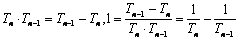 ,即
,即 .
.
又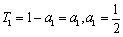 ,
,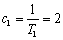
∴数列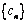 是以2为首项,1为公差的等差数列.
是以2为首项,1为公差的等差数列.
②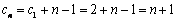 ,
,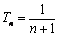 ,
,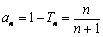 .
.
(2)∵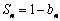 ,
,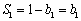
∴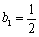 ,
,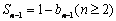 ,
,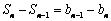 ,
,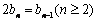
∴数列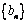 是以
是以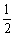 为首项,
为首项,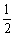 为公比的等比数列.
为公比的等比数列.
∴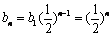 .
.
∵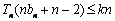 对
对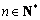 恒成立
恒成立
∴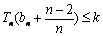 对
对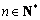 恒成立,即
恒成立,即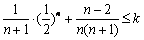 对
对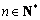 恒成立
恒成立
设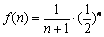 ,则
,则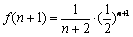
∵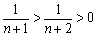 ,
,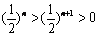 ,∴
,∴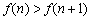
∴当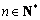 时,
时,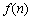 单调递减.
单调递减.
设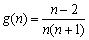 ,则
,则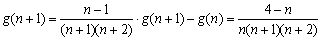
∴当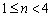 时,
时,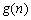 单调递增;
单调递增;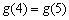 ;当
;当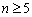 时,
时,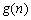 单调递减
单调递减
设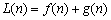 ,则
,则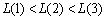 ,
,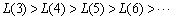
∴ 最大,且
最大,且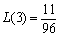 .∴实数
.∴实数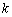 的取值范围为
的取值范围为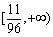 .
.

练习册系列答案
相关题目
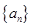 的前n项积为
的前n项积为 ;数列
;数列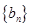 的前n项和为
的前n项和为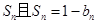 .
.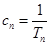 .①证明数列
.①证明数列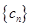 成等差数列;②求证数列
成等差数列;②求证数列 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. }的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn>
}的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn>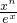 .
.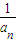 }的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn>
}的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn>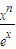 .
.