题目内容
(本题满分12分)
在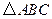 中,内角
中,内角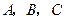 对边的边长分别是
对边的边长分别是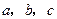 ,且满足
,且满足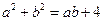 ,
,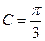 。
。
(1)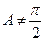 时,若
时,若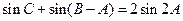 ,求
,求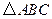 的面积.
的面积.
(2)求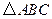 的面积等于
的面积等于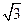 的一个充要条件。
的一个充要条件。
在
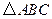 中,内角
中,内角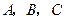 对边的边长分别是
对边的边长分别是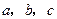 ,且满足
,且满足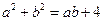 ,
,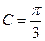 。
。(1)
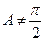 时,若
时,若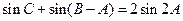 ,求
,求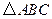 的面积.
的面积.(2)求
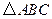 的面积等于
的面积等于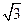 的一个充要条件。
的一个充要条件。(1) ,(2)
,(2)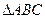 是边长为
是边长为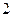 的正三角形。
的正三角形。
 ,(2)
,(2)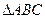 是边长为
是边长为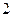 的正三角形。
的正三角形。(1)由题意得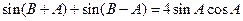 ,
,
即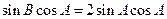 ,
,
由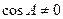 时,得
时,得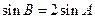 ,由正弦定理得
,由正弦定理得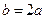 ,(3分)
,(3分)
联立方程组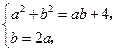 解得
解得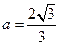 ,
,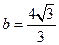 .
.
所以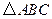 的面积
的面积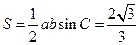 .(6分)
.(6分)
(2)若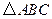 的面积等于
的面积等于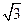 ,则
,则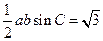 ,得
,得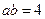 .
.
联立方程组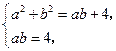 解得
解得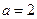 ,
,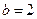 ,即
,即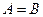 ,又
,又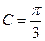 ,
,
故此时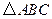 为正三角形,故
为正三角形,故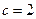 ,即当三角形面积为
,即当三角形面积为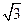 时,
时,
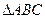 是边长为
是边长为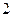 的正三角形。(10分)
的正三角形。(10分)
反之若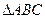 是边长为
是边长为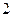 的正三角形,则其面积为
的正三角形,则其面积为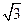 。(12分)
。(12分)
故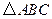 的面积等于
的面积等于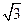 的一个充要条件是:
的一个充要条件是: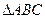 是边长为
是边长为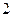 的正三角形。
的正三角形。
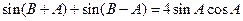 ,
,即
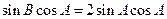 ,
,由
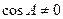 时,得
时,得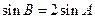 ,由正弦定理得
,由正弦定理得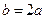 ,(3分)
,(3分)联立方程组
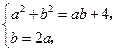 解得
解得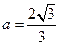 ,
,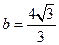 .
.所以
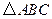 的面积
的面积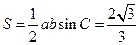 .(6分)
.(6分)(2)若
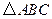 的面积等于
的面积等于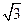 ,则
,则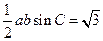 ,得
,得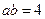 .
.联立方程组
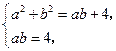 解得
解得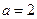 ,
,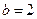 ,即
,即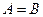 ,又
,又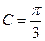 ,
,故此时
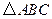 为正三角形,故
为正三角形,故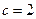 ,即当三角形面积为
,即当三角形面积为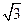 时,
时,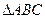 是边长为
是边长为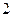 的正三角形。(10分)
的正三角形。(10分)反之若
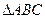 是边长为
是边长为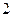 的正三角形,则其面积为
的正三角形,则其面积为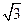 。(12分)
。(12分)故
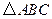 的面积等于
的面积等于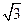 的一个充要条件是:
的一个充要条件是: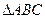 是边长为
是边长为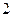 的正三角形。
的正三角形。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则
,则 的最大值是
的最大值是 B.
B. C.
C. D.
D.
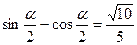 ,
, ,求
,求 的值.
的值.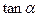 =2,求:
=2,求: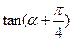 的值; (2)
的值; (2)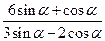 的值.
的值. 且
且 .求
.求 的值.
的值. ( )
( ) 的值为 ( )
的值为 ( )
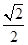

 ,求
,求 的值.
的值. 的值.
的值.