题目内容
若x,y∈R,集合A={(x,y)|x2+y2=1},B={(x,y)|ax+by=1,a>0,b>0},且A∩B至多有一个元素,则A∩B应满足的关系为________.
a2+b2≤1(a>0,b>0)
分析:由已知中集合A={(x,y)|x2+y2=1},B={(x,y)|ax+by=1,a>0,b>0},我们可得A∩B的元素即为圆x2+y2=1与直线ax+by=1,a>0,b>0的交点,根据A∩B至多有一个元素,可得圆心(0,0)到直线ax+by-1=0的距离不小于1,进而可得A∩B应满足的关系.
解答:∵集合A={(x,y)|x2+y2=1}表示以原点为圆心,以1为半径的圆
B={(x,y)|ax+by=1,a>0,b>0}表示一条直线
若A∩B至多有一个元素,
则直线与圆相切或相离
即圆心(0,0)到直线ax+by-1=0的距离不小于1
即d=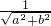 ≥1(a>0,b>0)
≥1(a>0,b>0)
即a2+b2≤1(a>0,b>0)
故答案为:a2+b2≤1(a>0,b>0)
点评:本题考查的知识点是集合关系中的参数取值问题,直线与圆的位置关系,集合交集的定义,其中正确理解A∩B至多有一个元素,表示圆心(0,0)到直线ax+by-1=0的距离不小于1,并由此构造出不等式是解答本题的关键.解答时易忽略已知中a>0,b>0的限制,而错解为a2+b2≤1.
分析:由已知中集合A={(x,y)|x2+y2=1},B={(x,y)|ax+by=1,a>0,b>0},我们可得A∩B的元素即为圆x2+y2=1与直线ax+by=1,a>0,b>0的交点,根据A∩B至多有一个元素,可得圆心(0,0)到直线ax+by-1=0的距离不小于1,进而可得A∩B应满足的关系.
解答:∵集合A={(x,y)|x2+y2=1}表示以原点为圆心,以1为半径的圆
B={(x,y)|ax+by=1,a>0,b>0}表示一条直线
若A∩B至多有一个元素,
则直线与圆相切或相离
即圆心(0,0)到直线ax+by-1=0的距离不小于1
即d=
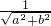 ≥1(a>0,b>0)
≥1(a>0,b>0)即a2+b2≤1(a>0,b>0)
故答案为:a2+b2≤1(a>0,b>0)
点评:本题考查的知识点是集合关系中的参数取值问题,直线与圆的位置关系,集合交集的定义,其中正确理解A∩B至多有一个元素,表示圆心(0,0)到直线ax+by-1=0的距离不小于1,并由此构造出不等式是解答本题的关键.解答时易忽略已知中a>0,b>0的限制,而错解为a2+b2≤1.

练习册系列答案
相关题目