题目内容
(本题满分12分)
记函数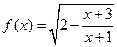 的定义域为A,
的定义域为A,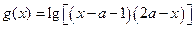 (
(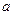 <1) 的定义域为B.
<1) 的定义域为B.
(1) 求A;
(2) 若B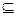 A, 求实数
A, 求实数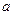 的取值范围.
的取值范围.
记函数
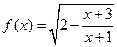 的定义域为A,
的定义域为A,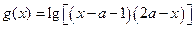 (
(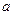 <1) 的定义域为B.
<1) 的定义域为B.(1) 求A;
(2) 若B
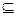 A, 求实数
A, 求实数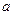 的取值范围.
的取值范围.(1)A=(-∞,-1)∪[1,+ ∞]
(2)实数a的取值范围是(-∞,-2)∪[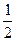 ,1]
,1]
(2)实数a的取值范围是(-∞,-2)∪[
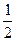 ,1]
,1]解:(1)2- ≥0, 得
≥0, 得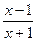 ≥0, x<-1或x≥1
≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞]…………………………………5分
(2) 由(x-a-1)(2a-x)>0, 得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a, ∴B="(2a,a+1)." …………………………………8分
∵B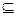 A, ∴2a≥1或a+1≤-1, 即a≥
A, ∴2a≥1或a+1≤-1, 即a≥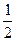 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴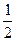 ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B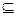 A时, 实数a的取值范围是
A时, 实数a的取值范围是
(-∞,-2)∪[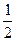 ,1]………………………………………12分
,1]………………………………………12分
 ≥0, 得
≥0, 得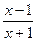 ≥0, x<-1或x≥1
≥0, x<-1或x≥1即A=(-∞,-1)∪[1,+ ∞]…………………………………5分
(2) 由(x-a-1)(2a-x)>0, 得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a, ∴B="(2a,a+1)." …………………………………8分
∵B
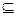 A, ∴2a≥1或a+1≤-1, 即a≥
A, ∴2a≥1或a+1≤-1, 即a≥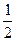 或a≤-2, 而a<1,
或a≤-2, 而a<1,∴
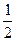 ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B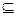 A时, 实数a的取值范围是
A时, 实数a的取值范围是(-∞,-2)∪[
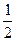 ,1]………………………………………12分
,1]………………………………………12分
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
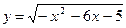 的值域为 .
的值域为 . 的定义域为M,
的定义域为M,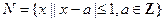 ,若
,若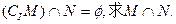
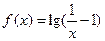 定义域是( )
定义域是( )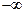 ,1)
,1)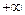 ]
]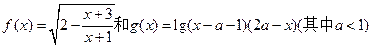 的定义域分别为A和B,若
的定义域分别为A和B,若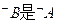 成立的必要不充分条件,求a的取值范围。
成立的必要不充分条件,求a的取值范围。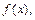 对任意的
对任意的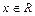 都有
都有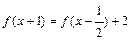 恒成立,且
恒成立,且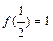 ,则
,则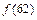 等于 ( )
等于 ( ) 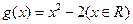 ,
, ,则
,则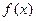 的值域是
的值域是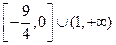
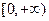

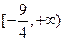
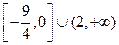
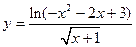 的定义域为 。
的定义域为 。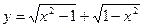 的定义域为( )
的定义域为( )