题目内容
试问能否找到一条斜率为k(k≠0)的直线l与椭圆| x2 | 3 |
分析:设直线l:y=kx+m为满足条件的直线,再设P为MN的中点,欲满足条件,只要AP⊥MN即可.由
得(1+3k2)x2+6mkx+3m2-3=0.然后利用韦达定理和根与系数的关系能够推导出当k∈(-1,0)∪(0,1)时,存在满足条件的直线l.
|
解答:解:设直线l:y=kx+m为满足条件的直线,再设P为MN的中点,欲满足条件,只要AP⊥MN即可
由
得(1+3k2)x2+6mkx+3m2-3=0.
设M(x1,y1),N(x2,y2),
则xp=
=-
,yp=kxp+m=
,∴kAP=
.∵AP⊥MN∴
=-
(k≠0),
故m=-
.
由△=36m2k2-4(1+3k2)(3m2-3)=9(1+3k2).(1-k2)>0,
得-1<k<1,且k≠0.
故当k∈(-1,0)∪(0,1)时,存在满足条件的直线l.
由
|
设M(x1,y1),N(x2,y2),
则xp=
| x1+x2 |
| 2 |
| 3mk |
| 1+3k2 |
| m |
| 1+3k2 |
| 3k2-m+1 |
| 3mk |
| 3k2-m+1 |
| 3mk |
| 1 |
| k |
故m=-
| 3k2+1 |
| 2 |
由△=36m2k2-4(1+3k2)(3m2-3)=9(1+3k2).(1-k2)>0,
得-1<k<1,且k≠0.
故当k∈(-1,0)∪(0,1)时,存在满足条件的直线l.
点评:本题考查直线和圆锥曲线的综合运用,解题时要合理地进行等价转化,注意韦达定理和根与系数的关系的灵活运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
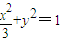 交于两个不同点M,N,且使M,N,且使M,N到点A(0,1)的距离相等,若存在,试求出k的取值范围;若不存在,请说明理由.
交于两个不同点M,N,且使M,N,且使M,N到点A(0,1)的距离相等,若存在,试求出k的取值范围;若不存在,请说明理由.