题目内容
求:(1)过A(2,
思路分析:(1)在直线上任意取一点M,根据已知条件想办法找到变量ρ、θ之间的关系.可以通过图中的直角三角形来解决,因为已知OA的长度,还知∠AOx=![]() ,还可以得到MH的长度,从而在Rt△OMH中找到变量ρ、θ之间的关系.
,还可以得到MH的长度,从而在Rt△OMH中找到变量ρ、θ之间的关系.
(2)在三角形中利用正弦定理来找到变量ρ、θ之间的关系.
解:(1)如图1-3-1所示,在直线l上任意取点M(ρ,θ),∵A(2,![]() ),
),
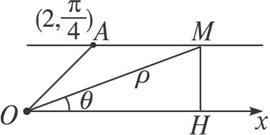
图1-3-1
∴|MH|=2·sin![]() =
=![]() .在Rt△OMH中,|MH|=|OM|sinθ,即ρsinθ=
.在Rt△OMH中,|MH|=|OM|sinθ,即ρsinθ=![]() ,
,
∴过A(2,![]() )平行于极轴的直线方程为ρsinθ=
)平行于极轴的直线方程为ρsinθ=![]() .
.
(2)如图1-3-2所示,A(3,![]() ),|OA|=3,∠AOB=
),|OA|=3,∠AOB=![]() ,由已知∠MBx=
,由已知∠MBx=![]() ,
,
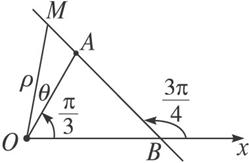
图1-3-2
∴∠OAB=![]() -
-![]() =
=![]() .
.
∴∠OAM=π-![]() .
.
又∠OMA=∠MBx-θ=![]() -θ.在△MOA中,
-θ.在△MOA中,
根据正弦定理得 ,
,
∵sin![]() =sin(
=sin(![]() +
+![]() )=
)=![]() ,
,
将sin(![]() -θ)展开,化简上面的方程,可得ρ(sinθ+cosθ)=
-θ)展开,化简上面的方程,可得ρ(sinθ+cosθ)=![]() .
.
∴过A(3,![]() )且和极轴成
)且和极轴成![]() 的直线为ρ(sinθ+cosθ)=
的直线为ρ(sinθ+cosθ)=![]() .
.
深化升华 可以看到,在求曲线方程时,要找出曲线上的点满足的几何条件,将它用坐标表示,再通过代数变换进行化简.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: