题目内容
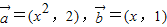
(1)若
 ,求x;
,求x;(2)若函数
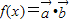 对应的图象记为C
对应的图象记为C(I)求曲线C在A(1,3)处的切线方程?
(II)若直线l为曲线C的切线,并且直线l与曲线C有且仅有一个公共点,求所有这样直线l的方程?
【答案】分析:(1)根据两个向量平行的坐标表示,列出关于x的方程,解之即可得到实数x的值;
(2)由向量数量积的坐标表示,得y=f(x)=x2•x+1×2=x3+2
(I)求出导数f'(x)在x=3处的函数值,即得切线的斜率,再用直线方程的点斜式列式,化简整理即可得到曲线C在A(1,3)处的切线方程;
(II)设切点坐标P(t,t3+2),得曲线C在点P处的切线方程为y=3t2x-2t3+2.将此切线方程与y=f(x)联解,所得方程有唯一实数根,可得t=0.由此即可得到
解答:解:(1)∵ ,且
,且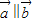
∴x2•1=2•x,解之得x=0或2
(2)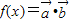 =x2•x+1×2=x3+2
=x2•x+1×2=x3+2
(I)对f(x)求导数,得f'(x)=3x2,
∴曲线C:y=f(x)在A(1,3)处切线的斜率k=f'(1)=3
结合直线的点斜式方程,得切线方程是y-3=3(x-1),即y=3x.
(II)设切点坐标P(t,t3+2),得在点P处切线的斜率k=f'(t)=3t2.
∴曲线C在点P处的切线方程为y-(t3+2)=3t2(x-t),即y=3t2x-2t3+2
由 得3t2x-2t3+2=x3+2,即x3-3t2x+2t3=0
得3t2x-2t3+2=x3+2,即x3-3t2x+2t3=0
∴(x-t)2(x+2t)=0,
因为切线与曲线C有且仅有一条一个公共点,所以只有t=0时以上方程有相等的实数根,此时l方程为y=2
∴存在直线l为曲线C的切线,并且直线l与曲线C有且仅有一个公共点,此时切线方程为y=2.
点评:本题以向量的坐标运算为载体,求三次多项式函数图象的切线问题,着重考查了平面向量的坐标表示和利用导数研究曲线的切线等知识,属于中档题.
(2)由向量数量积的坐标表示,得y=f(x)=x2•x+1×2=x3+2
(I)求出导数f'(x)在x=3处的函数值,即得切线的斜率,再用直线方程的点斜式列式,化简整理即可得到曲线C在A(1,3)处的切线方程;
(II)设切点坐标P(t,t3+2),得曲线C在点P处的切线方程为y=3t2x-2t3+2.将此切线方程与y=f(x)联解,所得方程有唯一实数根,可得t=0.由此即可得到
解答:解:(1)∵
 ,且
,且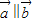
∴x2•1=2•x,解之得x=0或2
(2)
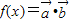 =x2•x+1×2=x3+2
=x2•x+1×2=x3+2(I)对f(x)求导数,得f'(x)=3x2,
∴曲线C:y=f(x)在A(1,3)处切线的斜率k=f'(1)=3
结合直线的点斜式方程,得切线方程是y-3=3(x-1),即y=3x.
(II)设切点坐标P(t,t3+2),得在点P处切线的斜率k=f'(t)=3t2.
∴曲线C在点P处的切线方程为y-(t3+2)=3t2(x-t),即y=3t2x-2t3+2
由
 得3t2x-2t3+2=x3+2,即x3-3t2x+2t3=0
得3t2x-2t3+2=x3+2,即x3-3t2x+2t3=0∴(x-t)2(x+2t)=0,
因为切线与曲线C有且仅有一条一个公共点,所以只有t=0时以上方程有相等的实数根,此时l方程为y=2
∴存在直线l为曲线C的切线,并且直线l与曲线C有且仅有一个公共点,此时切线方程为y=2.
点评:本题以向量的坐标运算为载体,求三次多项式函数图象的切线问题,着重考查了平面向量的坐标表示和利用导数研究曲线的切线等知识,属于中档题.

练习册系列答案
相关题目
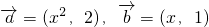
 ,求x;
,求x; 对应的图象记为C
对应的图象记为C
 ,求x;
,求x;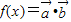 对应的图象记为C
对应的图象记为C