Question

函数为常数）是奇函数。（1）求实数m的值和函数 的图象与横轴的交点坐标。（2）设，求的最大值F（t）； （3）求F（t）的最小值。

Answer 1

解：（1）由于为奇函数，易得m=0

设

①当3t<0时，上述方程只有一个实数根x=0，所以与x轴的交点坐标为（0，0）

②当3t=0时，上述方程有三个相等实数根x=0，所以与x轴的交点坐标为（0，0）

③当3t>0时，上述方程的解为x₁=0，x₂，x ₃=，所以与横轴的交点坐标分别为（0，0），（，0），（－，0）

（2）显然是偶函数，

所以只要求出的最大值即可

又

①为增函数，  ∴

∴

②t>0时，则在[0，1]上

（i）即时，则在[0，1]上为减函数

∴，

故

（ii）0<t<1时，则在[0，1]上

x	0	（0，）		（，1）	1
		―	0	+
	0	↓	极小值 －2t	↑	1－3t

所以可以画出的草图如下，并且由图可知：

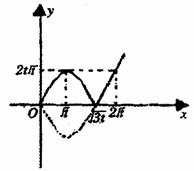
（1⁰）当

（2⁰）当

综上所述：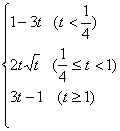

（3）显然上为减函数，

在上为增函数，

即在为增函数