题目内容
若以连续掷两次骰子分别得到的点数m、n作为点P的坐标 ,求:
,求:
(1)点P在直线 上的概率;
上的概率;
(2)点P在圆 外的概率。
外的概率。
 ,求:
,求:(1)点P在直线
 上的概率;
上的概率;(2)点P在圆
 外的概率。
外的概率。(1) 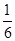 ;(2)
;(2) 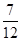 。
。
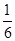 ;(2)
;(2) 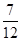 。
。试题分析:(1)
| | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
 有6个,一共有36数据 4分
有6个,一共有36数据 4分所以P点在直线
 上的概率为 6/36=1/6. 2分
上的概率为 6/36=1/6. 2分(2)在圆内的点P有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),
(2,3),(2,4)(3,1),(3,2),(3,3),(4,1),(4,2) 2分
在圆上的点P有 (3,4),(4,3) 1分
上述共有15个点在圆内或圆外。共有36个点坐标。 1分
所以点P在圆
 外的概率为 1-15/36=7/12 -2分
外的概率为 1-15/36=7/12 -2分点评:计算古典概型所包含基本事件总数的方法:(1)树形图;(2)列表法;(3)也可以用坐标系中的点表示;(4)用排列、组合求基本事件的总数。

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
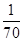 ”,根据这位负责人的话可以推断出参加面试的人数为( ).
”,根据这位负责人的话可以推断出参加面试的人数为( ).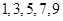 ,从这
,从这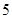 条线段中任取
条线段中任取 条,则所取
条,则所取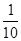
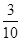
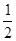
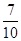
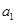 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),记出现向上的点数分别为
,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),记出现向上的点数分别为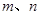 ,如果
,如果 是偶数,则把
是偶数,则把 ,对
,对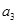 .当
.当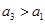 时,甲获胜,否则乙获胜.若甲获胜的概率为
时,甲获胜,否则乙获胜.若甲获胜的概率为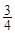 ,则
,则