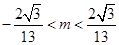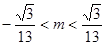题目内容
已知椭圆 ,则当在此椭圆上存在不同两点关于直线y=4x+m对称时m的取值范围为
,则当在此椭圆上存在不同两点关于直线y=4x+m对称时m的取值范围为
- A.

- B.
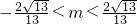
- C.
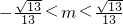
- D.

B
分析:设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),利用平方差法与直线y=4x+m可求得x0=-m,y0=-3m,点M(x0,y0)在椭圆内部,将其坐标代入椭圆方程即可求得m的取值范围.
解答:∵ ,故3x2+4y2-12=0,
,故3x2+4y2-12=0,
设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),
则 3 +4
+4 =12,①
=12,①
3 +4
+4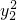 =12 ②
=12 ②
①-②得:3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,即 3•2x0•(x1-x2)+4•2y0•(y1-y2)=0,
∴ =-
=- •
•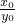 =-
=- .
.
∴y0=3x0,代入直线方程y=4x+m得x0=-m,y0=-3m;
因为(x0,y0)在椭圆内部,
∴3m2+4•(-3m)2<12,即3m2+36m2<12,解得- <m<
<m< .
.
故选B.
点评:本题考查直线与圆锥曲线的综合问题,着重考查平方差法的应用,突出化归思想的考查,属于难题.
分析:设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),利用平方差法与直线y=4x+m可求得x0=-m,y0=-3m,点M(x0,y0)在椭圆内部,将其坐标代入椭圆方程即可求得m的取值范围.
解答:∵
 ,故3x2+4y2-12=0,
,故3x2+4y2-12=0,设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),
则 3
 +4
+4 =12,①
=12,①3
 +4
+4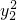 =12 ②
=12 ②①-②得:3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,即 3•2x0•(x1-x2)+4•2y0•(y1-y2)=0,
∴
 =-
=- •
•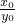 =-
=- .
.∴y0=3x0,代入直线方程y=4x+m得x0=-m,y0=-3m;
因为(x0,y0)在椭圆内部,
∴3m2+4•(-3m)2<12,即3m2+36m2<12,解得-
 <m<
<m< .
.故选B.
点评:本题考查直线与圆锥曲线的综合问题,着重考查平方差法的应用,突出化归思想的考查,属于难题.

练习册系列答案
相关题目
 ,则当在此椭圆上存在不同两点关于直线
,则当在此椭圆上存在不同两点关于直线 对称时
对称时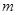 的取值
的取值 范
范 围为( )
围为( )  B.
B.
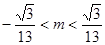 D.
D.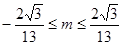
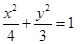 ,则当在此椭圆上存在不同两点关于直线
,则当在此椭圆上存在不同两点关于直线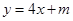 对称时
对称时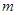 的取值范围为( )
的取值范围为( )