题目内容
(本题满分14分)求ax2+2x+1=0(a≠0)至少有一负根的充要条件。
a<0或0<a≤1
解:若方程有一正根和一负根,等价于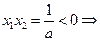 a<0
a<0
若方程有两负根,等价于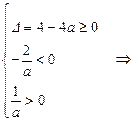 0<a≤1
0<a≤1
综上可知,原方程至少有一负根的必要条件是a<0或0<a≤1
由以上推理的可逆性,知当a<0时方程有异号两根;当0<a≤1时,方程有两负根
故a<0或0<a≤1是方程ax2+2x+1=0至少有一负根的充分条件
所以ax2+2x+1=0(a≠0)至少有一负根的充要条件是a<0或0<a≤1
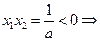 a<0
a<0 若方程有两负根,等价于
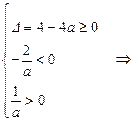 0<a≤1
0<a≤1综上可知,原方程至少有一负根的必要条件是a<0或0<a≤1
由以上推理的可逆性,知当a<0时方程有异号两根;当0<a≤1时,方程有两负根

故a<0或0<a≤1是方程ax2+2x+1=0至少有一负根的充分条件

所以ax2+2x+1=0(a≠0)至少有一负根的充要条件是a<0或0<a≤1

练习册系列答案
相关题目
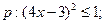 命题
命题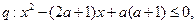 若
若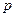 是
是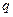 的充分不必要条件,求实数
的充分不必要条件,求实数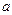 的取值范围.
的取值范围.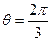 ”是“
”是“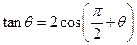 ”的 ( ).
”的 ( ).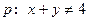 ,
,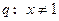 或
或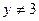 ,则p是q的( )
,则p是q的( ) 充分而不必要条件
充分而不必要条件  必要而不充分条件
必要而不充分条件 充要条件
充要条件  既不充分也不必要条件
既不充分也不必要条件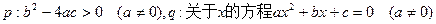 有实根,则p是q的 ( )
有实根,则p是q的 ( )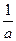 >-1”是“
>-1”是“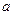 <-1”的成立的( )条件
<-1”的成立的( )条件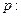 函数
函数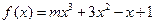 在
在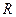 上是减函数,
上是减函数,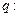
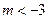 ,则
,则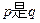 的( )
的( )