题目内容
已知函数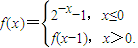 ,y=g(x)为k(x)=lnx+a+1在x=1处的切线方程,若方程f(x)-g(x)=0有且只有两个不相等的实数根,则实数a的取值范围是( )
,y=g(x)为k(x)=lnx+a+1在x=1处的切线方程,若方程f(x)-g(x)=0有且只有两个不相等的实数根,则实数a的取值范围是( )A.(-∞,1)
B.(-∞,1]
C.(0,1)
D.[0,+∞)
【答案】分析:由y=g(x)为k(x)=lnx+a+1在x=1处的切线方程,求得g(x)=x+a.我们在同一坐标系中画出函数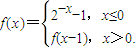 的图象与函数y=x+a的图象,利用数形结合,我们易求出满足条件实数a的取值范围.
的图象与函数y=x+a的图象,利用数形结合,我们易求出满足条件实数a的取值范围.
解答:解:∵k(x)=lnx+a+1,
∴k′(x)=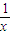 ,k(1)=a+1,
,k(1)=a+1,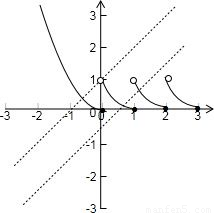
∴k′(1)=1,
∴k(x)=lnx+a+1在x=1处的切线方程为y-a-1=x-1,
∴g(x)=x+a.
函数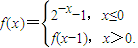 的图象如图所示,
的图象如图所示,
当a<1时,函数y=f(x)的图象与函数y=x+a的图象有两个交点,
即方程f(x)=x+a有且只有两个不相等的实数根.
所以实数a的取值范围是(-∞,1).
故选A.
点评:本题考查的知识点是根的存在性及根的个数的判断,考查导数的几何意义的应用.将方程f(x)=x+a根的个数,转化为求函数零点的个数,并用图象法进行解答是本题的关键.
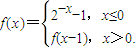 的图象与函数y=x+a的图象,利用数形结合,我们易求出满足条件实数a的取值范围.
的图象与函数y=x+a的图象,利用数形结合,我们易求出满足条件实数a的取值范围.解答:解:∵k(x)=lnx+a+1,
∴k′(x)=
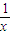 ,k(1)=a+1,
,k(1)=a+1,
∴k′(1)=1,
∴k(x)=lnx+a+1在x=1处的切线方程为y-a-1=x-1,
∴g(x)=x+a.
函数
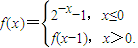 的图象如图所示,
的图象如图所示,当a<1时,函数y=f(x)的图象与函数y=x+a的图象有两个交点,
即方程f(x)=x+a有且只有两个不相等的实数根.
所以实数a的取值范围是(-∞,1).
故选A.
点评:本题考查的知识点是根的存在性及根的个数的判断,考查导数的几何意义的应用.将方程f(x)=x+a根的个数,转化为求函数零点的个数,并用图象法进行解答是本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目