题目内容
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk=| 1 |
| 2 |
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足
| bk+1 |
| bk |
| k-n |
| ab+1 |
分析:(Ⅰ)由ak=Sk-Sk-1=
akak+1-
ak-1ak,得ak(ak+1-ak-1)=2ak.再由ak+1-ak-1=2.知a2m-1=1+(m-1)•2=2m-1.a2m=2+(m-1)•2=2m,m∈N*.由此可知ak=k(k∈N*).
(Ⅱ)由题意知bk=
•
••
•b1=(-1)k-1•
•1=(-1)k-1•
(k=1,2,n).由此可求出b1+b2+b3+…+bn的值.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由题意知bk=
| bk |
| bk-1 |
| bk-1 |
| bk-2 |
| b2 |
| b1 |
| (n-k+1)(n-k+2)(n-1) |
| k•(k-1)••2•1 |
| 1 |
| n |
| C | k n |
解答:解:(Ⅰ)当k=1,由a1=S1=
a1a2及a1=1,得a2=2.
当k≥2时,由ak=Sk-Sk-1=
akak+1-
ak-1ak,得ak(ak+1-ak-1)=2ak.
因为ak≠0,所以ak+1-ak-1=2.
从而a2m-1=1+(m-1)•2=2m-1.
a2m=2+(m-1)•2=2m,m∈N*.
故ak=k(k∈N*).
(Ⅱ)因为ak=k,所以
=-
=-
.
所以bk=
•
•…•
•b1=(-1)k-1•
•1=(-1)k-1•
(k=1,2,n).
故b1+b2+b3+…+bn=
[
-
+
-+(-1)n-1
]=
{1-[
-
+
-+(-1)n•
]}=
.
| 1 |
| 2 |
当k≥2时,由ak=Sk-Sk-1=
| 1 |
| 2 |
| 1 |
| 2 |
因为ak≠0,所以ak+1-ak-1=2.
从而a2m-1=1+(m-1)•2=2m-1.
a2m=2+(m-1)•2=2m,m∈N*.
故ak=k(k∈N*).
(Ⅱ)因为ak=k,所以
| bk+1 |
| bk |
| n-k |
| ak+1 |
| n-k |
| k+1 |
所以bk=
| bk |
| bk-1 |
| bk-1 |
| bk-2 |
| b2 |
| b1 |
| (n-k+1)(n-k+2)…(n-1) |
| k•(k-1)•…•2•1 |
| 1 |
| n |
| C | k n |
故b1+b2+b3+…+bn=
| 1 |
| n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| 1 |
| n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| 1 |
| n |
点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
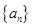 的前
的前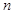 项和为
项和为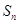 ,且
,且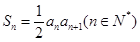 ,其中
,其中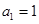
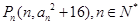 ,试求直线
,试求直线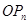 斜率的最小值(
斜率的最小值(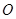 为坐标原点).
为坐标原点). N*),其中a1=1.
N*),其中a1=1. (k=1,2,…,n-1),b1=1.
(k=1,2,…,n-1),b1=1.