题目内容
17.已知在数列{an}中,a1=2,an=$\frac{n+1}{n-1}$an-1,求通项公式an.分析 根据数列的递推关系,利用累积法进行求解即可.
解答 解:∵a1=2,an=$\frac{n+1}{n-1}$an-1,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n-1}$,
则当n≥3时,
an=a2•$\frac{{a}_{3}}{{a}_{2}}$$•\frac{{a}_{4}}{{a}_{3}}$…$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{3}{1}×2$•$\frac{4}{2}$$•\frac{5}{3}•\frac{6}{4}…$$\frac{n-1}{n-3}$$•\frac{n}{n-2}•\frac{n+1}{n-1}$=n(n+1),
当n=2时,a2=$\frac{3}{1}×2=6$,满足an=n(n+1),
a1=2,满足an=n(n+1),
综上数列的通项公式为an=n(n+1).
点评 本题主要考查数列通项公式的求解,利用累积法是解决本题的关键.

练习册系列答案
相关题目
7.抛物线x2=-8y的焦点坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (0,4) | D. | (0,-4) |
2.若(x2+$\frac{3}{x}$)n展开式中的二项式系数之和为64,则展开式的常数项为( )
| A. | 1215 | B. | 9 | C. | 27 | D. | 1 |
9.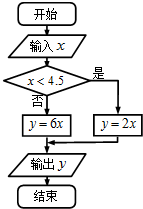 如图所示的是根据输入的x值计算y的值的程序框图,若x依次取数列$\left\{{\frac{{{n^2}+5}}{n}}\right\}(n∈{{N}^*})$中的项,则所得y值的最小值为( )
如图所示的是根据输入的x值计算y的值的程序框图,若x依次取数列$\left\{{\frac{{{n^2}+5}}{n}}\right\}(n∈{{N}^*})$中的项,则所得y值的最小值为( )
 如图所示的是根据输入的x值计算y的值的程序框图,若x依次取数列$\left\{{\frac{{{n^2}+5}}{n}}\right\}(n∈{{N}^*})$中的项,则所得y值的最小值为( )
如图所示的是根据输入的x值计算y的值的程序框图,若x依次取数列$\left\{{\frac{{{n^2}+5}}{n}}\right\}(n∈{{N}^*})$中的项,则所得y值的最小值为( )| A. | 28 | B. | 27 | C. | 9 | D. | 4$\sqrt{5}$ |
7.已知点F是双曲线$\frac{x{\;}^{2}}{a{\;}^{2}}$-$\frac{y{\;}^{2}}{b{\;}^{2}}$=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,以坐标原点O为圆心,OF为半径的圆与该双曲线左支交于点A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( )
| A. | (1,1+$\sqrt{3}$) | B. | (1,$\sqrt{2}$) | C. | (1,1+$\sqrt{2}$) | D. | (2,1+$\sqrt{2}$) |
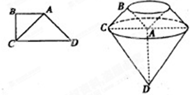 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周得到如图所示的几何体σ.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周得到如图所示的几何体σ.