题目内容
 对于函数f(x)=(asin x+cos x)cos x-
对于函数f(x)=(asin x+cos x)cos x-| 1 |
| 2 |
| π |
| 6 |
(1)求a的值;
(2)作出函数f(x)在x∈[0,π]上的图象(不要求书写作图过程).
(3)根据画出的图象写出函数y=f(x)在[0,π]上的单调区间和最值.
分析:(1)f(x)=(asin x+cos x)cos x-
=
sin2x+
cos2x,由f(
)=1能求出a=
.
(2)由f(x)=sin(2x+
),能作出函数f(x)在x∈[0,π]上的图象.
(3)结合图象,能够写出函数y=f(x)在[0,π]上的单调区间和最值.
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 3 |
(2)由f(x)=sin(2x+
| π |
| 6 |
(3)结合图象,能够写出函数y=f(x)在[0,π]上的单调区间和最值.
解答:解:(1)f(x)=(asin x+cos x)cos x-
=asinxcosx+cos2x-
=
sin2x+
-
=
sin2x+
cos2x,
∵f(
)=1,∴
sin
+
cos
=1,
即
•
+
•
=1,解得a=
.…(4分)
(2)由(1)知,f(x)=sin(2x+
)
函数f(x)在x∈[0,π]上的图象如右图,
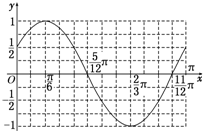 …(8分)
…(8分)
(3)由图可知,y=f(x)在[0,π]上的增区间为[0,
],[
π,π],
减区间为[
,
π]…(10分)
当x=
时,f(x)max=1;当x=
π时,f(x)min=-1.…(12分)
| 1 |
| 2 |
=asinxcosx+cos2x-
| 1 |
| 2 |
=
| a |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
=
| a |
| 2 |
| 1 |
| 2 |
∵f(
| π |
| 6 |
| a |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
即
| a |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
(2)由(1)知,f(x)=sin(2x+
| π |
| 6 |
函数f(x)在x∈[0,π]上的图象如右图,
 …(8分)
…(8分)(3)由图可知,y=f(x)在[0,π]上的增区间为[0,
| π |
| 6 |
| 2 |
| 3 |
减区间为[
| π |
| 6 |
| 2 |
| 3 |
当x=
| π |
| 6 |
| 2 |
| 3 |
点评:本题考查三角函数的图象和性质的应用,解题时要认真审题,仔细解答,注意三角函数恒等变换的合理运用.

练习册系列答案
相关题目