题目内容

(1)a =" ln" 3
(2)an =(m-
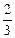 )· 4n-1 +
)· 4n-1 +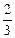
(1)∵ 函数f (x) 在x = 1处连续,f(1)= 2×1 + 1 = 3,
∴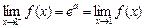 , 3 = ea,∴ a =" ln" 3. ………… 5分
, 3 = ea,∴ a =" ln" 3. ………… 5分
(2)∵ 对任意n有an>1,∴ f (2an-1) =" 2" (2an-1) + 1 = 4an-1,
于是an+1 = f(2an-1)-1 =(4an-1)-1 = 4an-2,
∴ an+1-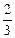 = 4(an-
= 4(an-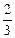 ),表明数列 { an-
),表明数列 { an-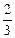 }是以a1-
}是以a1-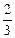 = m-
= m-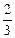 为首项,4为公比的等比数列,于是 an-
为首项,4为公比的等比数列,于是 an-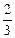 =(m-
=(m-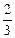 )· 4n-1,
)· 4n-1,
从而an =(m-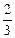 )· 4n-1 +
)· 4n-1 +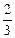 . …………………… 12分
. …………………… 12分
∴
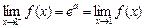 , 3 = ea,∴ a =" ln" 3. ………… 5分
, 3 = ea,∴ a =" ln" 3. ………… 5分(2)∵ 对任意n有an>1,∴ f (2an-1) =" 2" (2an-1) + 1 = 4an-1,
于是an+1 = f(2an-1)-1 =(4an-1)-1 = 4an-2,
∴ an+1-
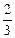 = 4(an-
= 4(an-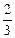 ),表明数列 { an-
),表明数列 { an-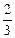 }是以a1-
}是以a1-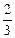 = m-
= m-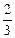 为首项,4为公比的等比数列,于是 an-
为首项,4为公比的等比数列,于是 an-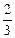 =(m-
=(m-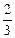 )· 4n-1,
)· 4n-1,从而an =(m-
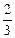 )· 4n-1 +
)· 4n-1 +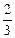 . …………………… 12分
. …………………… 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
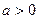 ,且
,且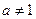 ,
,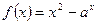 ,当
,当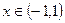 时均有
时均有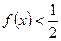 ,则实数
,则实数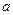 范围是 ( )
范围是 ( ) 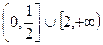 (
(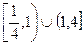
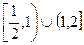
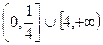
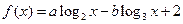 ,若
,若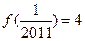 ,则
,则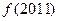 的值为_________
的值为_________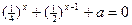 有正数解,则实数
有正数解,则实数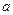 的取值范围是 ( )
的取值范围是 ( )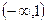
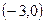

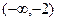
 函数f(x)=|x2-2|,若f(a)≥f(b),且0≤a≤b,则满足条件的点(a,b)所围成区域的面积为 ;
函数f(x)=|x2-2|,若f(a)≥f(b),且0≤a≤b,则满足条件的点(a,b)所围成区域的面积为 ;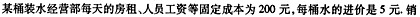
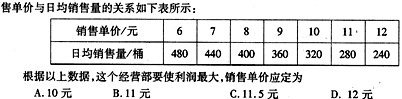
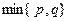 表示
表示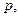
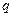 两者中较小的一个,若函数
两者中较小的一个,若函数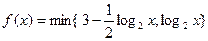 ,则满足
,则满足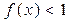 的
的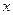 的取值范围是( )
的取值范围是( )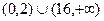
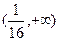

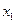 满足2x+
满足2x+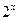 ="5,"
="5," 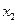 满足2x+2
满足2x+2 (x
(x 1)="5," 则
1)="5," 则