题目内容
 (2012•台州一模)已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是( )
(2012•台州一模)已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是( )分析:三视图可知该几何体是由一个圆柱和半球组成的组成体,圆柱的底面直径等于半球的直径为4,圆柱的高h=2,代入圆柱的体积公式和半球的体积公式,即可得到答案.
解答: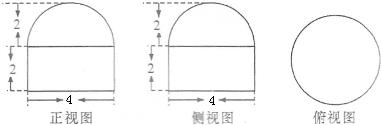 解:由已知中的三视图可得:
解:由已知中的三视图可得:
该几何体是由一个圆柱和半球组成的组成体
由图中所示的数据可得:
圆柱的底面直径等于半球的直径为4,则半径R=2,
圆柱的高h=2,
∴V圆柱=πR2h=π×22×2=8πcm3
V半球=
×
πR3=
πcm3
故该几何体的体积V=8π+
π=
cm3.
故选C.
 解:由已知中的三视图可得:
解:由已知中的三视图可得:该几何体是由一个圆柱和半球组成的组成体
由图中所示的数据可得:
圆柱的底面直径等于半球的直径为4,则半径R=2,
圆柱的高h=2,
∴V圆柱=πR2h=π×22×2=8πcm3
V半球=
| 1 |
| 2 |
| 4 |
| 3 |
| 16 |
| 3 |
故该几何体的体积V=8π+
| 16 |
| 3 |
| 40 |
| 3 |
故选C.
点评:本题考查的知识点是由三视图求体积,其中根据已知中的三视图判断出几何体的形状是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目