题目内容
将直线y=-5x+15绕着它与x轴的交点按逆时针方向旋转α角后,恰好与圆(x+2)2+(y+1)2=13相切,则α的一个值是( )A.30°
B.45°
C.60°
D.90°
【答案】分析:令直线y=-5x+15中y=0,求出x的值,确定出直线与x轴的交点坐标,设出切线的斜率为k,表示出切线的方程,再根据圆的标准方程找出圆心坐标和圆的半径,根据点到直线的距离表示出圆心到切线的距离d,使d等于圆的半径列出关于k的方程,求出方程的解得到k的值,取k的一个值,代入到角公式即可求出tanα的值,由α的范围,利用特殊角的三角函数值即可得到α的度数.
解答:解:因为直线与x轴的交点为(3,0),
所以设切线方程为y=k(x-3),又已知圆的圆心(-2,-1),半径为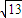 ,
,
由圆心到直线的距离等于半径可知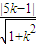 =
=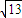 ,
,
解得k=- ,和k=
,和k= ,
,
由题设可知应取k=- ,
,
由到角公式知tanα=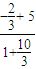 =1,
=1,
则旋转角α的一个值为45°.
故选B
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,直线的点斜式方程,圆的标准方程,以及到角公式的运用,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练运用此性质是解本题的关键.
解答:解:因为直线与x轴的交点为(3,0),
所以设切线方程为y=k(x-3),又已知圆的圆心(-2,-1),半径为
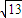 ,
,由圆心到直线的距离等于半径可知
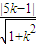 =
=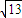 ,
,解得k=-
 ,和k=
,和k= ,
,由题设可知应取k=-
 ,
,由到角公式知tanα=
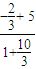 =1,
=1,则旋转角α的一个值为45°.
故选B
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,直线的点斜式方程,圆的标准方程,以及到角公式的运用,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练运用此性质是解本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目