题目内容
某简谐运动的图象对应的函数函数解析式为:f(x)=3sin(
+
)-1
(1)指出f(x)的周期、振幅、频率、相位、初相;
(2)用五点法画出它在一个周期内的闭区间上的图象;
(3)求函数图象的对称中心和对称轴.
| x |
| 2 |
| π |
| 6 |
(1)指出f(x)的周期、振幅、频率、相位、初相;
(2)用五点法画出它在一个周期内的闭区间上的图象;
(3)求函数图象的对称中心和对称轴.
分析:(1)由f(x)=3sin(
+
)-1,可知f(x)的周期、振幅、频率、相位、初相;
(2)分别令
+
=0,
,π,
,2π,得到相应的x的值,列表,利用五点法即可画出它在一个周期内的闭区间上的图象;
(3)利用正弦函数的图象与性质可求得该函数图象的对称中心和对称轴.
| x |
| 2 |
| π |
| 6 |
(2)分别令
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
(3)利用正弦函数的图象与性质可求得该函数图象的对称中心和对称轴.
解答:解:(1)∵f(x)=3sin(
+
)-1,
∴其周期T=4π,振幅为3,频率为
、相位是
+
,初相为
;
(2)分别令
+
=0,
,π,
,2π,得到相应的x的值,列表如下:
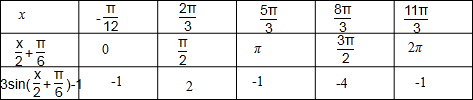
作图象如下:
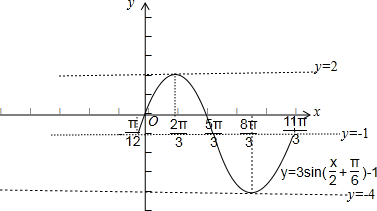
(3)由
+
=kπ+
(k∈Z)得:x=2kπ+
(k∈Z),
∴其对称轴方程为:x=2kπ+
(k∈Z);
由
+
=kπ(k∈Z)得:x=2kπ-
(k∈Z),
∴函数f(x)=3sin(
+
)-1的图象的对称中心为(2kπ-
,-1)(k∈Z).
| x |
| 2 |
| π |
| 6 |
∴其周期T=4π,振幅为3,频率为
| 1 |
| 4π |
| x |
| 2 |
| π |
| 6 |
| π |
| 6 |
(2)分别令
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |

作图象如下:

(3)由
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
∴其对称轴方程为:x=2kπ+
| 2π |
| 3 |
由
| x |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴函数f(x)=3sin(
| x |
| 2 |
| π |
| 6 |
| π |
| 3 |
点评:本题考查函数y=Asin(ωx+φ)的图象性质,着重考查“五点法”作图与正弦函数图象的性质,属于中档题.

练习册系列答案
相关题目
 sin(2x-
sin(2x- ).
).