题目内容
(本小题满分12分)
设平面向量 = ( m , -1),
= ( m , -1),  =" (" 2 , n ),其中 m, n
=" (" 2 , n ),其中 m, n {-2,-1,1,2}.
{-2,-1,1,2}.
(1)记“使得 //
// 成立的( m,n)”为事件A,求事件A发生的概率;
成立的( m,n)”为事件A,求事件A发生的概率;
(2)记“使得 ⊥(
⊥( -2
-2 )成立的( m,n)”为事件B,求事件B发生的概率.
)成立的( m,n)”为事件B,求事件B发生的概率.
设平面向量
 = ( m , -1),
= ( m , -1),  =" (" 2 , n ),其中 m, n
=" (" 2 , n ),其中 m, n {-2,-1,1,2}.
{-2,-1,1,2}.(1)记“使得
 //
// 成立的( m,n)”为事件A,求事件A发生的概率;
成立的( m,n)”为事件A,求事件A发生的概率;(2)记“使得
 ⊥(
⊥( -2
-2 )成立的( m,n)”为事件B,求事件B发生的概率.
)成立的( m,n)”为事件B,求事件B发生的概率.(1)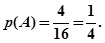 (2)
(2)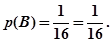
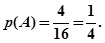 (2)
(2)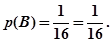
(1)先求出总的基本事件的个数为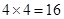 种,然后再求出满足
种,然后再求出满足 //
// 即满足mn=-2的基本事件的个数为4个.根据古典事件的概率计算公式计算即可.
即满足mn=-2的基本事件的个数为4个.根据古典事件的概率计算公式计算即可.
(2) 使得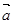 ⊥(
⊥(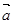 -2
-2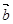 )也就是
)也就是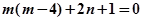 即:
即: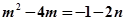 .这个满足这个条件的基本事件只有1个.所以此事件的概率为
.这个满足这个条件的基本事件只有1个.所以此事件的概率为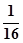 .
.
解:(1)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),(2,-1),(2,1),(2,2)共有16种. ………2分
使得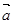 //
//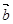 成立的( m,n),满足:mn=-2
成立的( m,n),满足:mn=-2
事件A有(-2,1),(-1,2),(1,-2),(2,-1)4种. ……………4分
故所求的概率为: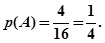 ……………………6分
……………………6分
(2)使得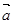 ⊥(
⊥(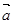 -2
-2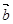 )成立的( m,n)满足:
)成立的( m,n)满足:
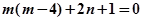 即:
即: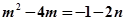 ………9分
………9分
事件B有:(1,1)一种 ……………………………10分
故所求的概率为: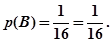 …………………………………12分
…………………………………12分
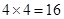 种,然后再求出满足
种,然后再求出满足 //
// 即满足mn=-2的基本事件的个数为4个.根据古典事件的概率计算公式计算即可.
即满足mn=-2的基本事件的个数为4个.根据古典事件的概率计算公式计算即可.(2) 使得
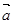 ⊥(
⊥(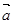 -2
-2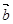 )也就是
)也就是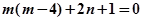 即:
即: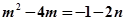 .这个满足这个条件的基本事件只有1个.所以此事件的概率为
.这个满足这个条件的基本事件只有1个.所以此事件的概率为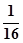 .
.解:(1)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),(2,-1),(2,1),(2,2)共有16种. ………2分
使得
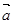 //
//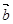 成立的( m,n),满足:mn=-2
成立的( m,n),满足:mn=-2 事件A有(-2,1),(-1,2),(1,-2),(2,-1)4种. ……………4分
故所求的概率为:
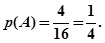 ……………………6分
……………………6分(2)使得
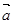 ⊥(
⊥(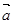 -2
-2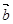 )成立的( m,n)满足:
)成立的( m,n)满足: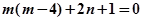 即:
即: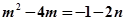 ………9分
………9分事件B有:(1,1)一种 ……………………………10分
故所求的概率为:
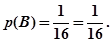 …………………………………12分
…………………………………12分
练习册系列答案
相关题目
 则顶点D的坐标为( )
则顶点D的坐标为( )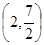
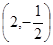

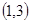
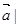 ="8,"
="8," 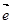 为单位向量,当它们的夹角为
为单位向量,当它们的夹角为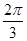 时,
时,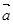 在
在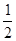
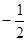
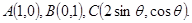
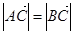 ,求
,求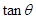 的值;
的值;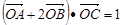 ,其中
,其中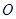 为坐标原点,求
为坐标原点,求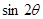 的值
的值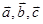 均为单位向量,且
均为单位向量,且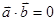 ,
,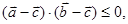 则
则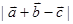 的最大值为( )
的最大值为( )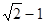
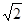
 ⊥
⊥ ,则
,则 =________
=________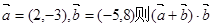 等于( )
等于( ) , 若
, 若 , 则
, 则 等于( )
等于( )


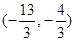
 ,
,  ,
,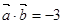 ,则
,则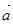 与
与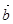 的夹角是
的夹角是