题目内容
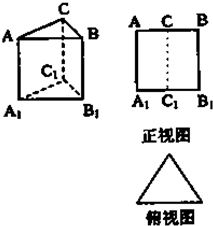 如图,水平放置的三棱柱的侧棱长和底面边长均2,且侧棱AA1⊥面
如图,水平放置的三棱柱的侧棱长和底面边长均2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形.
(1)求该三棱柱的侧视图的面积;
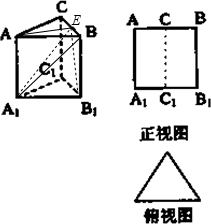
(2)若E为边BC的中点,求三棱锥A1-B1BE的体积.
分析:(1)根据俯视图为边长为2的等边三角形,求出三角形的高即为侧视图的宽,再根据正视图为边长为2的正方形,可知侧视图的高为2,计算可求侧视图的面积.
(2)根据三棱柱为直三棱柱,可证AE⊥平面BEB1,求得三棱锥的高与底面面积,代入体积公式计算.
(2)根据三棱柱为直三棱柱,可证AE⊥平面BEB1,求得三棱锥的高与底面面积,代入体积公式计算.
解答:解:(1)三棱柱的底面为等边三角形,边长为2,作出等边三角形的高后,组成直角三角形,
∵底边的一半为1,∴等边三角形的高为
,
由题意知左视图是一个高为2,宽为
的矩形,
∴三棱柱的侧视图的面积为2
.
(2)∵侧棱AA1⊥平面A1B1C1,∴三棱柱为直棱柱,
又E为BC的中点,∴AE⊥平面BEB1,∴AE为三棱锥A1-B1BE的高,
AE=
,S△BB1E=
×1×2=1,
∴三棱锥A1-B1BE的体积V=
×1×
=
.
∵底边的一半为1,∴等边三角形的高为
| 3 |
由题意知左视图是一个高为2,宽为
| 3 |
∴三棱柱的侧视图的面积为2
| 3 |
(2)∵侧棱AA1⊥平面A1B1C1,∴三棱柱为直棱柱,
又E为BC的中点,∴AE⊥平面BEB1,∴AE为三棱锥A1-B1BE的高,
AE=
| 3 |
| 1 |
| 2 |
∴三棱锥A1-B1BE的体积V=
| 1 |
| 3 |
| 3 |
| ||
| 3 |

点评:考查由三视图求几何体的体积,考查了三视图的识别能力,作图能力,三视图的投影规则是主视、俯视 长对正;主视、左视高平齐,左视、俯视宽相等.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
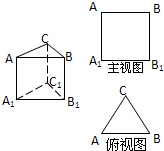 如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,主视图是边长为2的正方形,则该三棱柱的左视图周长为( )
如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,主视图是边长为2的正方形,则该三棱柱的左视图周长为( )| A、8 | ||
B、4+2
| ||
C、4+2
| ||
D、4
|
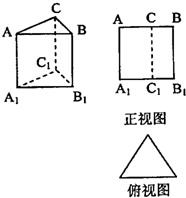 如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为
如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为 (2012•淄博一模)如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为( )
(2012•淄博一模)如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为( ) 如图,水平放置的三棱柱侧棱AA1⊥面A1B1C1,正视图是边长为1的正方形,俯视图是边长为1的正三角形,则该三棱柱的侧视图面积为( )
如图,水平放置的三棱柱侧棱AA1⊥面A1B1C1,正视图是边长为1的正方形,俯视图是边长为1的正三角形,则该三棱柱的侧视图面积为( )