题目内容
某人从2008年起,每年1月1日到银行新存入 元(一年定期),若年利率为
元(一年定期),若年利率为 保持不变,且每年到期存款和利息自动转为新的一年定期,到2011年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2011年底将所有存款及利息全部取回,则可取回的钱数(元)为
A.  | B.  |
C. | D. |
A
解析试题分析:因为根据题意可知,银行存款是按照复利计算,那么
008年的a元到了2008年底本息和a(1+r)
2008年底本息和a(1+r)到了2009年底本息和为a(1+r)2,
22009年底本息和为a(1+r)2到了2010年底本息和为a(1+r)3,
2010年底本息和为a(1+r)3到了2011年底本息和为a(1+r)4,
所有金额为a(1+r)+a(1+r)2+a(1+r)3+ a(1+r)4,则根据等比数列的前n项和可知结论为
 ,故选A.
,故选A.
考点:本试题主要考查了数列的应用,以及等比数列的求和,同时考查了计算能力,属于中档题.
点评:解决该试题的关键是先分别计算每一年存入a元到2011年的本息和,然后将所有存款的本息相加,根据等比数列求得求和公式解之即可.

练习册系列答案
相关题目
已知函数 ,则
,则 等于( )
等于( )
| A.4 | B. | C. | D. |
已知关于 的二次函数
的二次函数 在区间
在区间 上是单调函数,则
上是单调函数,则 的取值范围是( )
的取值范围是( )
A.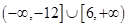 | B. |
C. | D. |
若 ,则【 】
,则【 】
A. | B. | C.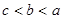 | D. |
幂函数 图象过点
图象过点 ,则
,则
A. | B.3 | C. | D. |
设函数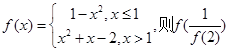 的值为( )
的值为( )
A. | B. | C. | D. |
 、
、 、
、 、
、 在同一坐标系中的图象如图所示,则
在同一坐标系中的图象如图所示,则 与1的大小关系为 ( )
与1的大小关系为 ( )




 ,则函数
,则函数 与
与 的图象可能是下列四个选项中的( )
的图象可能是下列四个选项中的( )
 与
与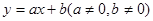 的函数图象只可能是( )
的函数图象只可能是( )