题目内容
甲,乙两队各有3名队员,投篮比赛时,每个队员各投一次,命中率均为 ,
,(1)设前n(n=1,2,3,4,5,6)个人的进球总数与n之比为an,求满足条件a6=
 ,且an≤
,且an≤ (n=1,2,3,4,5)的概率;
(n=1,2,3,4,5)的概率;(2)设甲,乙两队进球数分别为i,j(i,j∈{0,1,2,3}),记ξ=|i-j|,求随机变量ξ的分布列和数学期望.
【答案】分析:(1)a6= ,即6个人投篮进了3个球,又an≤
,即6个人投篮进了3个球,又an≤ (n=1,2,3,4,5),则有两种情况:第一,第1人投篮没投进,第2人投篮投进了,第3人投篮没投进,第4、5人总共投进了1个球,第6人投篮投进了,求出概率P1,第二,第1人投篮没投进,第2人投篮没投进,第3、4、5人总共投进了2个球,第6人投篮投进了,求出概率为P2,根据互斥事件的概率公式可求出所求概率为P=P1+P2;
(n=1,2,3,4,5),则有两种情况:第一,第1人投篮没投进,第2人投篮投进了,第3人投篮没投进,第4、5人总共投进了1个球,第6人投篮投进了,求出概率P1,第二,第1人投篮没投进,第2人投篮没投进,第3、4、5人总共投进了2个球,第6人投篮投进了,求出概率为P2,根据互斥事件的概率公式可求出所求概率为P=P1+P2;
(2)ξ的取值可能为0,1,2,3,然后利用n次独立重复试验中恰好发生k次的概率公式求出相应的概率,列出分布列,最后利用数学期望公式解之即可.
解答:解:(1)a6= ,即6个人投篮进了3个球,
,即6个人投篮进了3个球,
又an≤ (n=1,2,3,4,5),则有两种情况:
(n=1,2,3,4,5),则有两种情况:
第一,第1人投篮没投进,第2人投篮投进了,第3人投篮没投进,第4、5人总共投进了1个球,第6人投篮投进了,其概率为P1= ×
× ×
× ×C21(
×C21( )2×
)2× =
=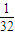
第二,第1人投篮没投进,第2人投篮没投进,第3、4、5人总共投进了2个球,第6人投篮投进了,其概率为P2= ×
× ×C32(
×C32( )3×
)3× =
=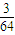
从而,所求概率为P=P1+P2=
(2)ξ的取值可能为0,1,2,3
P(ξ=0)表示两队进球数相同,即有
P(ξ=0)=( )3×(
)3×( )3+C31(
)3+C31( )3×C31(
)3×C31( )3+C32(
)3+C32( )3×C32(
)3×C32( )3+(
)3+( )3×(
)3×( )3=
)3=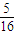
P(ξ=1)=2[( )3×C31(
)3×C31( )3+C31(
)3+C31( )3×C32(
)3×C32( )3+C32(
)3+C32( )3×(
)3×( )3]=
)3]=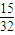
P(ξ=2)=2[( )3×C32(
)3×C32( )3+C31(
)3+C31( )3×(
)3×( )3]=
)3]=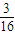
P(ξ=3)=2[( )3×(
)3×( )3]=
)3]=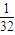
∴Eξ=0×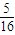 +1×
+1×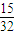 +2×
+2×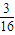 +3×
+3×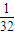 =
=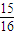
点评:本题主要考查了n次独立重复试验中恰好发生k次的概率,以及离散型随机变量的期望和分布列,同时考查了计算能力和分类讨论的数学思想,属于中档题.
 ,即6个人投篮进了3个球,又an≤
,即6个人投篮进了3个球,又an≤ (n=1,2,3,4,5),则有两种情况:第一,第1人投篮没投进,第2人投篮投进了,第3人投篮没投进,第4、5人总共投进了1个球,第6人投篮投进了,求出概率P1,第二,第1人投篮没投进,第2人投篮没投进,第3、4、5人总共投进了2个球,第6人投篮投进了,求出概率为P2,根据互斥事件的概率公式可求出所求概率为P=P1+P2;
(n=1,2,3,4,5),则有两种情况:第一,第1人投篮没投进,第2人投篮投进了,第3人投篮没投进,第4、5人总共投进了1个球,第6人投篮投进了,求出概率P1,第二,第1人投篮没投进,第2人投篮没投进,第3、4、5人总共投进了2个球,第6人投篮投进了,求出概率为P2,根据互斥事件的概率公式可求出所求概率为P=P1+P2;(2)ξ的取值可能为0,1,2,3,然后利用n次独立重复试验中恰好发生k次的概率公式求出相应的概率,列出分布列,最后利用数学期望公式解之即可.
解答:解:(1)a6=
 ,即6个人投篮进了3个球,
,即6个人投篮进了3个球,又an≤
 (n=1,2,3,4,5),则有两种情况:
(n=1,2,3,4,5),则有两种情况:第一,第1人投篮没投进,第2人投篮投进了,第3人投篮没投进,第4、5人总共投进了1个球,第6人投篮投进了,其概率为P1=
 ×
× ×
× ×C21(
×C21( )2×
)2× =
=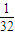
第二,第1人投篮没投进,第2人投篮没投进,第3、4、5人总共投进了2个球,第6人投篮投进了,其概率为P2=
 ×
× ×C32(
×C32( )3×
)3× =
=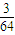
从而,所求概率为P=P1+P2=

(2)ξ的取值可能为0,1,2,3
P(ξ=0)表示两队进球数相同,即有
P(ξ=0)=(
 )3×(
)3×( )3+C31(
)3+C31( )3×C31(
)3×C31( )3+C32(
)3+C32( )3×C32(
)3×C32( )3+(
)3+( )3×(
)3×( )3=
)3=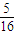
P(ξ=1)=2[(
 )3×C31(
)3×C31( )3+C31(
)3+C31( )3×C32(
)3×C32( )3+C32(
)3+C32( )3×(
)3×( )3]=
)3]=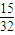
P(ξ=2)=2[(
 )3×C32(
)3×C32( )3+C31(
)3+C31( )3×(
)3×( )3]=
)3]=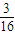
P(ξ=3)=2[(
 )3×(
)3×( )3]=
)3]=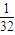
| ξ | 1 | 2 | 3 | |
| P | 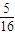 | 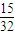 | 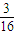 | 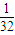 |
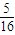 +1×
+1×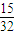 +2×
+2×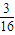 +3×
+3×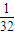 =
=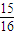
点评:本题主要考查了n次独立重复试验中恰好发生k次的概率,以及离散型随机变量的期望和分布列,同时考查了计算能力和分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目