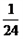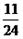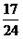题目内容
一道竞赛题,甲同学解出它的概率为
,乙同学解出它的概率为
,丙同学解出它的概率为
,则独立解答此题时,三人中只有一人解出的概率为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
分析:根据题意,只有一人解出的试题的事件包含甲解出而其余两人没有解出,乙解出而其余两人没有解出,丙解出而其余两人没有解出,三个互斥的事件,而三人解出答案是相互独立的,进而计算可得答案.
解答:解:根据题意,只有一人解出的试题的事件
包含甲解出而其余两人没有解出,乙解出而其余两人没有解出,丙解出而其余两人没有解出,三个互斥的事件,
而三人解出答案是相互独立的,
则P(只有一人解出试题)=
×
×
+
×
×
+
×
×
=
,
故选B.
包含甲解出而其余两人没有解出,乙解出而其余两人没有解出,丙解出而其余两人没有解出,三个互斥的事件,
而三人解出答案是相互独立的,
则P(只有一人解出试题)=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 11 |
| 24 |
故选B.
点评:本题考查相互独立事件的概率的乘法公式,注意先按互斥事件分类,再按相互独立事件的概率乘法公式进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,乙同学解出它的概率为
,乙同学解出它的概率为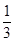 ,丙同学解出它的概率为
,丙同学解出它的概率为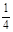 ,则独立解答此题时,三人中只有一人解出的概率为
,则独立解答此题时,三人中只有一人解出的概率为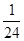 B.
B.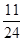 C.
C.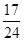 D.1
D.1 ,乙同学解出它的概率为
,乙同学解出它的概率为 ,丙同学解出它的概率为
,丙同学解出它的概率为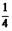 ,则独立解答此题时,三人中只有一人解出的概率为
,则独立解答此题时,三人中只有一人解出的概率为