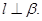题目内容
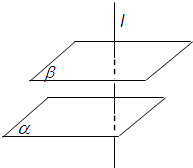 求证:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面.(要求:根据图形,写出已知、求证,并给出证明过程)
求证:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面.(要求:根据图形,写出已知、求证,并给出证明过程)分析:先写出已知、求证,再假设直线l与平面α、β分别相交于点A、B,过点A、B分别在两个平面内得a、b与c、d,根据α∥β,可得a∥c,b∥d,利用l⊥α且a、b?α
可得l⊥a,l⊥b,从而l⊥c,l⊥d,利用线面垂直的判定定理可得结论.
可得l⊥a,l⊥b,从而l⊥c,l⊥d,利用线面垂直的判定定理可得结论.
解答: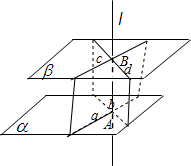 已知:α∥β,l⊥α,求证:l⊥β.
已知:α∥β,l⊥α,求证:l⊥β.
证明:假设直线l与平面α、β分别相交于点A、B,过点A、B分别在两个平面内得a、b与c、d,
∵α∥β,
∴a∥c,b∥d
∵l⊥α且a、b?α
∴l⊥a,l⊥b
又∵a∥c,b∥d
∴l⊥c,l⊥d
又∵c、d?β且c∩d=B
∴l⊥β.
 已知:α∥β,l⊥α,求证:l⊥β.
已知:α∥β,l⊥α,求证:l⊥β.证明:假设直线l与平面α、β分别相交于点A、B,过点A、B分别在两个平面内得a、b与c、d,
∵α∥β,
∴a∥c,b∥d
∵l⊥α且a、b?α
∴l⊥a,l⊥b
又∵a∥c,b∥d
∴l⊥c,l⊥d
又∵c、d?β且c∩d=B
∴l⊥β.
点评:本题考查面面平行的性质,考查线面垂直的性质与判定,正确运用面面平行的性质,线面垂直的判定定理是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 且
且 ,
, 求证:
求证: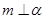
 求证:
求证: