题目内容
给定正整数n(n≥2)按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,n,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依此类推,最后一行(第n行)只有一个数,例如n=6时数表如图所,则当n=2009时最后一行的数是 .
【答案】分析:分析已知图形中的各行数据分析第一行的第一数的变化情况,可以得到a1=1,a2=3=1+2,a3=8=1+2×2+3,a4=20=1+2×2+2×3+4,…则an=Cn-1×1+Cn-11×2+…+Cn-1n-1×n,故不难求出当n=2009时最后一行的数a2009的值.
解答:解:邻第m行的第一个数为,am
∵可以得到a1=1,a2=3=1+2,a3=8=1+2×2+3,a4=20=1+3×2+3×3+4,…
则an=Cn-1×1+Cn-11×2+…+Cn-1n-1×n,
当n=2009时
最后一行的数
a2009=C2008×1+C20081×2+…+C20081×n=1005×22008
故答案为:1005×22008
点评:本题考查点是归纳与类比及二项式定理的相关运算,根据已知的数据,我们可以得到每一行第一个数的变化规律,根据规律我们可以计算出每一行的第一个数字,将n=2009代入公式,即可求解.
解答:解:邻第m行的第一个数为,am
∵可以得到a1=1,a2=3=1+2,a3=8=1+2×2+3,a4=20=1+3×2+3×3+4,…
则an=Cn-1×1+Cn-11×2+…+Cn-1n-1×n,
当n=2009时
最后一行的数
a2009=C2008×1+C20081×2+…+C20081×n=1005×22008
故答案为:1005×22008
点评:本题考查点是归纳与类比及二项式定理的相关运算,根据已知的数据,我们可以得到每一行第一个数的变化规律,根据规律我们可以计算出每一行的第一个数字,将n=2009代入公式,即可求解.

练习册系列答案
相关题目
 14、给定正整数n(n≥2)按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,n,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依次类推,最后一行(第n行)只有一个数,例如n=6时数表如图所,则当n=2009时最后一行的数是
14、给定正整数n(n≥2)按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,n,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依次类推,最后一行(第n行)只有一个数,例如n=6时数表如图所,则当n=2009时最后一行的数是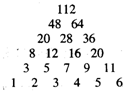 给定正整数n(n≥2)按图方式构成三角形数表:第一行依次写上数1,2,3,…,n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比下一行少一个数),依此类推,最后一行(第n行)只有一个数.例如n=6时数表如图所示,则当n=2010时最后一行的数是
给定正整数n(n≥2)按图方式构成三角形数表:第一行依次写上数1,2,3,…,n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比下一行少一个数),依此类推,最后一行(第n行)只有一个数.例如n=6时数表如图所示,则当n=2010时最后一行的数是 给定正整数n(n≥2)按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,n,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依此类推,最后一行(第n行)只有一个数,例如n=6时数表如图所,则当n=2009时最后一行的数是
给定正整数n(n≥2)按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,n,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依此类推,最后一行(第n行)只有一个数,例如n=6时数表如图所,则当n=2009时最后一行的数是