题目内容
(本题满分12分)
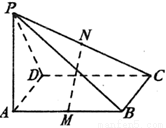
如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.
(1)求证:MN//平面PAD
(2)求证:MN⊥CD
(3)若∠PDA=45°,求证:MN⊥平面PCD.
【答案】
见解析。
【解析】本题考查证明线线垂直、线面垂直的方法,求棱锥的体积,证明AE⊥平面PCD 是解题的关键.
(1)取PD的中点E,连结AE、EN则有EN//CD//AB//AM,
且EN=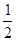 CD=
CD=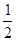 AB=MA.∴四边形AMNE是平行四边形.∴MN//AE.∵AE
AB=MA.∴四边形AMNE是平行四边形.∴MN//AE.∵AE 平面PAD,MN
平面PAD,MN 平面PAD,∴MN//平面PAD.
平面PAD,∴MN//平面PAD.
(2)∵PA⊥平面ABCD,∴PA⊥AB.又AD⊥AB,∴AB⊥平面PAD.∴AB⊥AE,即AB⊥MN.又CD//AB,∴MN⊥CD.
(3)取PD的中点E,证明AMNE为平行四边形,MN∥AE,由等腰直角三角形斜边上的中线性质可得AE⊥PD,再由CD⊥AE 可得AE⊥平面PCD,故有MN⊥平面PCD.
证明:(1)如图,
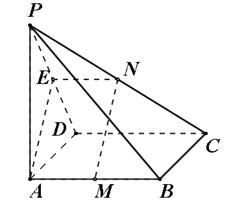
取PD的中点E,连结AE、EN则有EN//CD//AB//AM,
且EN=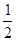 CD=
CD=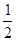 AB=MA.
AB=MA.
∴四边形AMNE是平行四边形.
∴MN//AE.
∵AE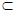 平面PAD,MN
平面PAD,MN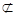 平面PAD,
平面PAD,
∴MN//平面PAD.
(2)∵PA⊥平面ABCD,∴PA⊥AB.
又AD⊥AB,∴AB⊥平面PAD.
∴AB⊥AE,即AB⊥MN.又CD//AB,
∴MN⊥CD.
(3)∵PA⊥平面ABCD,∴PA⊥AD.
又∠PAD=45°,E是PD中点,
∴AE⊥PD,即MN⊥PD.
又MN⊥CD,∴MN⊥平面PCD

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
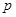 与死亡年数
与死亡年数 之间的函数关系式;
之间的函数关系式;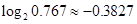 )
) 内接于圆
内接于圆 ,
, 是圆
是圆 为平行四边形,
为平行四边形, 平面
平面 ,
, ,
, 。
。 求三棱锥
求三棱锥 的体积
的体积 ;
; 。
。
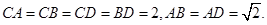
 平面BCD;
平面BCD;