题目内容
已知函数 ,
,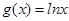 .
.
(1)设函数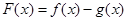 ,求函数
,求函数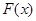 的单调区间;
的单调区间;
(2)是否存在实数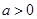 ,使得方程
,使得方程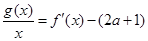 在区间
在区间 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出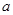 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】
(Ⅱ) (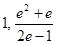 ) .
) .
【解析】
试题分析:(I)因为,函数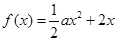 ,
,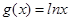 .
.
所以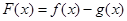 =
=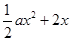 -lnx,其定义域为(0,+
-lnx,其定义域为(0,+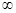 )。
)。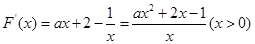 ,
,
当a=0时,由f′(x)>0,得,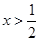 ,故f(x)在(
,故f(x)在(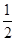 ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0,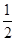 )单调递减;
)单调递减;
当a>0时,由f′(x)>0,得,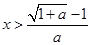 ,故f(x)在(
,故f(x)在(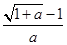 ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0,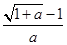 )单调递减;
)单调递减;
当a<0时,由f′(x)>0,得,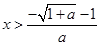 ,故f(x)在(
,故f(x)在(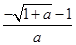 ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0,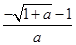 )单调递减。
)单调递减。
(Ⅱ)把方程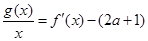 整理为
整理为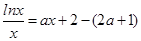 ,
,
即为方程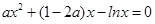 . 5分
. 5分
设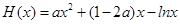
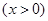 ,原方程在区间(
,原方程在区间(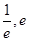 )内有且只有两个不相等的实数根, 即为函数
)内有且只有两个不相等的实数根, 即为函数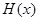 在区间(
在区间(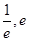 )内有且只有两个零点. 6分
)内有且只有两个零点. 6分
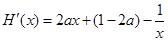
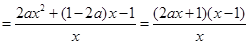 7分
7分
令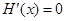 ,因为
,因为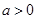 ,解得
,解得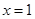 或
或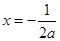 (舍) 8分
(舍) 8分
当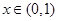 时,
时, 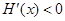 ,
, 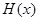 是减函数;当
是减函数;当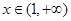 时,
时, 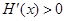 ,
,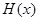 是增函数 10分
是增函数 10分
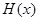 在(
在(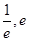 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需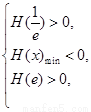
即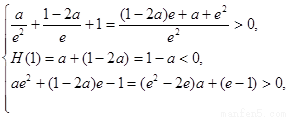 ∴
∴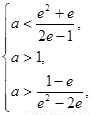
解得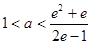 , 所以
, 所以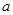 的取值范围是(
的取值范围是(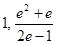 ) .
) .
考点:本题主要考查应用导数研究函数的单调性、最值及不等式恒成立问题,函数零点,不等式的解法。
点评:难题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。(I)中要对a的不同取值情况加以讨论,在解不等式取舍过程中易于出错。涉及不等式恒成立问题,转化成了研究函数的最值,通过构建a的不等式组,求得a的范围。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |