题目内容
函数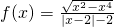 .给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)
.给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)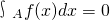 (其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则
(其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则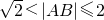 .请写出所有关于函数f(x)性质正确描述的序号______.
.请写出所有关于函数f(x)性质正确描述的序号______.
解:要使函数有意义,需满足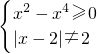 ,
,
解得-1≤x≤1且x≠0,即函数的定义域为[-1,0)∪(0,1],
故(1)不正确.
根据函数的定义域可将函数解析式化简为 ,
,
所以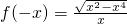 =-f(x),即函数是奇函数,所以其图象关于原点对称;
=-f(x),即函数是奇函数,所以其图象关于原点对称;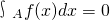 (其中A为函数的定义域),
(其中A为函数的定义域),
故(2)(4)正确.
因为函数的定义域是间断的,
故(3)的说法是错误的.
由于A、B为函数f(x)图象上任意不同两点,所以|AB|>0,而不是 ,
,
故(5)的说法是错误的.
所以答案为(2)(4).
分析:先求定义域,根据定义域化简函数解析式;根据函数单调性、奇偶性的定义判断单调性、奇偶性、研究长度;根据积分的几何意义求积分值.
点评:解决本题的关键是求出定义域后化简解析式,要是直接研究其性质会很麻烦.
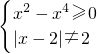 ,
,解得-1≤x≤1且x≠0,即函数的定义域为[-1,0)∪(0,1],
故(1)不正确.
根据函数的定义域可将函数解析式化简为
 ,
,所以
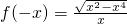 =-f(x),即函数是奇函数,所以其图象关于原点对称;
=-f(x),即函数是奇函数,所以其图象关于原点对称;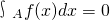 (其中A为函数的定义域),
(其中A为函数的定义域),故(2)(4)正确.
因为函数的定义域是间断的,
故(3)的说法是错误的.
由于A、B为函数f(x)图象上任意不同两点,所以|AB|>0,而不是
 ,
,故(5)的说法是错误的.
所以答案为(2)(4).
分析:先求定义域,根据定义域化简函数解析式;根据函数单调性、奇偶性的定义判断单调性、奇偶性、研究长度;根据积分的几何意义求积分值.
点评:解决本题的关键是求出定义域后化简解析式,要是直接研究其性质会很麻烦.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
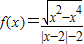 .给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)
.给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)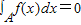 (其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则
(其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则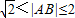 .请写出所有关于函数f(x)性质正确描述的序号 .
.请写出所有关于函数f(x)性质正确描述的序号 .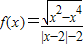 .给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)
.给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)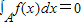 (其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则
(其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则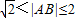 .请写出所有关于函数f(x)性质正确描述的序号 .
.请写出所有关于函数f(x)性质正确描述的序号 .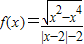 .给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)
.给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)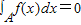 (其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则
(其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则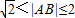 .请写出所有关于函数f(x)性质正确描述的序号 .
.请写出所有关于函数f(x)性质正确描述的序号 . .给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)
.给出函数f(x)下列性质:(1)函数的定义域和值域均为[-1,1];(2)函数的图象关于原点成中心对称;(3)函数在定义域上单调递增;(4)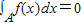 (其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则
(其中A为函数的定义域);(5)A、B为函数f(x)图象上任意不同两点,则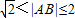 .请写出所有关于函数f(x)性质正确描述的序号 .
.请写出所有关于函数f(x)性质正确描述的序号 .