题目内容
点P是曲线f(x,y)=0上的动点,定点Q(1,1),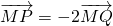 ,则点M的轨迹方程是________.
,则点M的轨迹方程是________.
f(3x-2,3y-2)=0
分析:分别设出点P、M的坐标,根据已知向量条件用点M的坐标表示点P的坐标,然后代入点P满足的方程即可得出.
解答:设点P(x0,y0),∵点P是曲线f(x,y)=0上的动点,∴f(x0,y0)=0.
设M(x,y),又Q(1,1),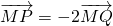 ,
,
∴(x0-x,y0-y)=-2(1-x,1-y),
即 ,解得
,解得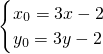 ,
,
代入f(x0,y0)=0得f(3x-2,3y-2)=0.
故点M的轨迹方程得f(3x-2,3y-2)=0.
故答案为f(3x-2,3y-2)=0.
点评:熟练掌握向量的相等和“代点法”是解题的关键.
分析:分别设出点P、M的坐标,根据已知向量条件用点M的坐标表示点P的坐标,然后代入点P满足的方程即可得出.
解答:设点P(x0,y0),∵点P是曲线f(x,y)=0上的动点,∴f(x0,y0)=0.
设M(x,y),又Q(1,1),
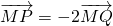 ,
,∴(x0-x,y0-y)=-2(1-x,1-y),
即
 ,解得
,解得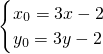 ,
,代入f(x0,y0)=0得f(3x-2,3y-2)=0.
故点M的轨迹方程得f(3x-2,3y-2)=0.
故答案为f(3x-2,3y-2)=0.
点评:熟练掌握向量的相等和“代点法”是解题的关键.

练习册系列答案
相关题目
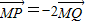 ,则点M的轨迹方程是 .
,则点M的轨迹方程是 .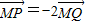 ,则点M的轨迹方程是 .
,则点M的轨迹方程是 .