题目内容
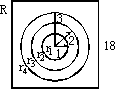
(意大利馅饼问题)山姆的意大利馅饼屋中设有一个投镖靶.该靶为正方形板,边长为18厘米,挂于前门附近的墙上,顾客花两角五分的硬币便可投一镖,并有机会赢得一种意大利馅饼中的一个.投镖靶中画有三个同心圆,圆心在靶的中心,当镖击中半径为1厘米的最内层圆形区域时,可得到一个大馅饼;当镖击中半径为1厘米到2厘米之间的环形区域时,可得到一个中馅饼;当镖击中半径为2厘米到3厘米之间的环形区域时,可得到一个小馅饼;如果镖击中靶上的其他部分,则得不到馅饼.假设每一位顾客都能投镖中靶,并且每个圆的周边线没有宽度,即每个镖不会击在线上,试求一位顾客赢得下列各种馅饼的概率:
(1)一个大馅饼;(2)一个中馅饼;(3)一个小馅饼;(4)没得到馅饼.
答案:
解析:
解析:
|
分析:镖可投在箭靶的任何位置,且击中任何位置的机会是相等的,属几何概型.将馅饼问题转化为对应几何图形的面积比是求解本题的关键. 解:如图,试验的全部结果构成的区域为一个边长为18厘米的正方形R,r1,r2,r3和r4分别表示事件得到一个大馅饼、中馅饼、小馅饼和没得到馅饼.
|

练习册系列答案
相关题目