题目内容
某商家经销一种销售成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500kg；销售单价每涨1元，月销售量就减少10kg，针对这种销售情况，
（1）设销售单价为每千克x元，月销售利润为y元，求y与x的函数关系式；
（2）商店想在月销售成本不超过10000元的情况下，使得月销售利润不少于8000元，销售单价应定为多少元时，利润最大？
解：（1）由题意可得：y=（x-40）[500-10（x-50）]=-10x2+1400x-40000．
（2）由题意可得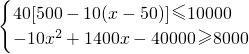
，
解得75≤x≤80．
∵y=-10x2+1400x-40000在[75，80]上单调递减，
∴销售单价应该定为75元时，利润最大．
分析：（1）根据利润=每kg的利润×销售量即可得出；
（2）由题意可得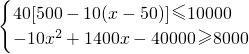，解出即可得出x的取值范围，再利用二次函数的单调性即可得出．
点评：正确理解利润=每kg的利润×销售量、二次函数的单调性、一元二次不等式的解法等是解题的关键．
（2）由题意可得
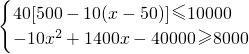，解得75≤x≤80．
∵y=-10x2+1400x-40000在[75，80]上单调递减，
∴销售单价应该定为75元时，利润最大．
分析：（1）根据利润=每kg的利润×销售量即可得出；
（2）由题意可得
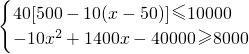，解出即可得出x的取值范围，再利用二次函数的单调性即可得出．点评：正确理解利润=每kg的利润×销售量、二次函数的单调性、一元二次不等式的解法等是解题的关键．
练习册系列答案
相关题目