题目内容
如图,已知菱形 ,其边长为2,
,其边长为2,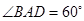 ,
,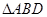 绕着
绕着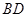 顺时针旋转
顺时针旋转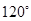 得到
得到 ,
,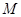 是
是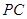 的中点.
的中点.
(1)求证: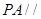 平面
平面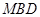 ;
;
(2)求直线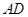 与平面
与平面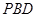 所成角的正弦值.
所成角的正弦值.
(1)利用线线平行证明线面平行;(2)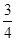 .
.
解析试题分析:(1)连接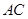 ,设
,设 ,连接
,连接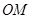 ,
,
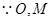 分别是
分别是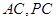 的中点,
的中点,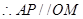 ,
,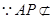 平面
平面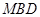 ,
,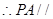 平面
平面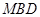 6分
6分
(2)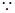 菱形
菱形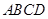 ,
, ,
,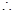
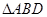 绕着
绕着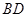 顺时针旋转
顺时针旋转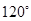 得到
得到
即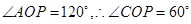 ,
, ,
, 直线
直线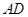 与平面
与平面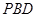 所成角为直线
所成角为直线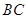 与平面
与平面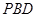 所成角 8分
所成角 8分
作 于
于 点,连接
点,连接 ,
,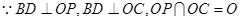 ,
,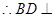 平面
平面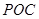 ,
, ,
, ,
, 平面
平面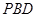 ,
,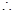 直线
直线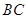 与平面
与平面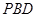 所成角为
所成角为 11分
11分
在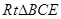 中,
中, ,
, ,
,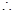 直线
直线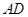 与平面
与平面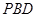 所成角的正弦值为
所成角的正弦值为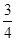 . 14分
. 14分
考点:本题考查了空间中的线面关系
点评:直线和平面成角的重点是研究斜线和平面成角,常规求解是采用“作、证、算”,但角不易作出时,可利用构成三条线段的本质特征求解,即分别求斜线段、射影线段、点A到平面的距离求之.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 的对棱
的对棱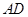 、
、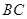 成
成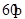 的角,且
的角,且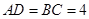 ,平行于
,平行于 、
、 、
、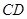 、
、 于
于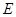 、
、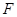 、
、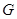 、
、 .
.
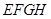 为平行四边形;
为平行四边形;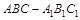 中,
中,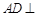 平面
平面 ,其垂足
,其垂足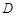 落在直线
落在直线 上.
上.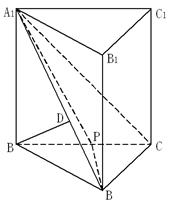
 ;
;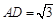 ,
,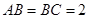 ,
,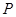 为
为 的中点,求三棱锥
的中点,求三棱锥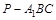 的体积.
的体积.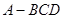 中,
中, 是
是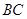 的中点,
的中点, ,
, ,
,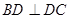 ,
,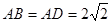 ,二面角
,二面角 的大小为
的大小为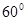 .
.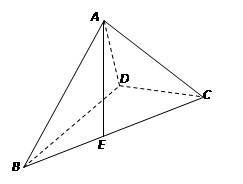
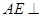 平面
平面 ;
;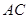 与平面
与平面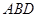 所成角的正弦值.
所成角的正弦值.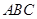 中,
中,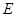 、
、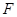 、
、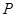 分别是
分别是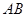 、
、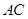 、
、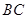 边上的点,满足
边上的点,满足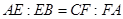
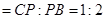 (如图1).将△
(如图1).将△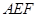 沿
沿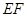 折起到
折起到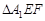 的位置,使二面角
的位置,使二面角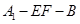 成直二面角,连结
成直二面角,连结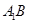 、
、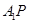 (如图2)
(如图2)
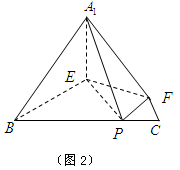
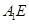 ⊥平面
⊥平面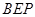 ;
;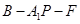 的余弦值.
的余弦值. 和矩形
和矩形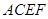 所在的平面互相垂直,
所在的平面互相垂直,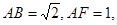
 是线段
是线段 的中点。
的中点。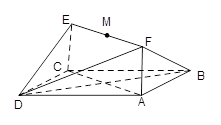
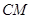 ∥平面
∥平面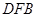
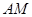 与
与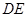 所成的角的余弦值。
所成的角的余弦值。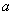 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=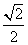 AD.
AD.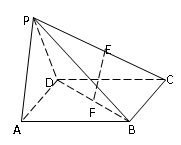
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD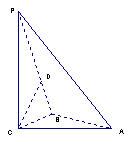
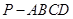 中,底面
中,底面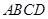 为矩
为矩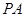 ⊥平面
⊥平面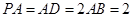 ,
,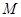 为
为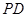 上的点,若
上的点,若
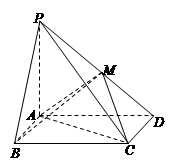
 的大小.
的大小.