题目内容
有一批食品出厂前要进行五项指标检验,若有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是0.2.
(I)求这批产品不能出厂的概率(保留三位有效数字);
(Ⅱ)求直至五项指标全部检验完毕,才能确定该批食品是否出厂的概率(保留两位有效数字).
(I)求这批产品不能出厂的概率(保留三位有效数字);
(Ⅱ)求直至五项指标全部检验完毕,才能确定该批食品是否出厂的概率(保留两位有效数字).
分析:(I)先求得这批食品能出厂的概率,再用1减去此概率概率,即得所求.
(Ⅱ)直到五项指标全部检验完毕,才能确定该批食品是否出厂,这说明前四项指标中只有一项是不合格的,再根据n次独立重复实验中恰好发生k次的概率公式,计算求得结果.
(Ⅱ)直到五项指标全部检验完毕,才能确定该批食品是否出厂,这说明前四项指标中只有一项是不合格的,再根据n次独立重复实验中恰好发生k次的概率公式,计算求得结果.
解答:解:(I)由题意可得,这批食品的合格率为0.8,求得这批食品能出厂的概率是 0.85+
×0.84×0.2,
故这批食品不能出厂的概率是P=1-0.85-
×0.84×0.2≈0.263.(4分)
(Ⅱ)直到五项指标全部检验完毕,才能确定该批食品是否出厂,说明前四项指标中只有一项不合格,
故所求的概率为
×0.2×0.83=0.4096.…(12分)
| C | 1 5 |
故这批食品不能出厂的概率是P=1-0.85-
| C | 1 5 |
(Ⅱ)直到五项指标全部检验完毕,才能确定该批食品是否出厂,说明前四项指标中只有一项不合格,
故所求的概率为
| C | 1 4 |
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,所求的事件的概率与它的对立事件的概率之间的关系,
属于中档题.
属于中档题.

练习册系列答案
相关题目
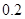 .
.